题目内容
(本小题满分12分)如图,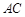 是圆
是圆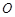 的直径,点
的直径,点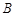 在圆
在圆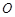 上,
上,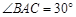 ,
,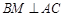 交
交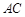 于点
于点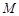 ,
,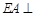 平面
平面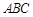 ,
,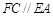 ,
,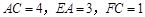 .
.
(Ⅰ)证明: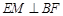 ;
;
(Ⅱ)求平面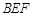 与平面
与平面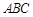 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.

【答案】
(1)见解析;(2)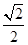 .
.
【解析】(I)本题主要思路还是通过证明线面垂直来证明线线垂直,本小题可以证明: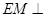 平面
平面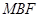 ,需证:
,需证: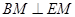 和
和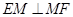 .
.
(II)本题可通过传统方法找到二面角的平面角,也可利用向量法求二面角.延长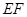 交
交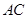 于
于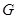 ,连
,连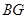 ,过
,过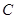 作
作 ,连结
,连结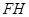 .可以证明
.可以证明 为平面
为平面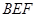 与平面
与平面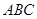 所成的二面角的平面角.然后解三角形即可求角.
所成的二面角的平面角.然后解三角形即可求角.
(法一)(Ⅰ)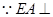 平面
平面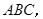
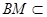 平面
平面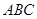 ,
,
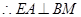 .………………………………………………1分
.………………………………………………1分
又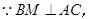
 ,
,
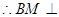 平面
平面
而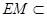 平面
平面
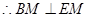 . ………………………………………………3分
. ………………………………………………3分
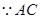 是圆
是圆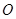 的直径,
的直径,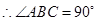 .
.
又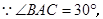
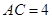 ,
,
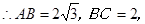
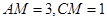 .
.
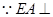 平面
平面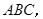
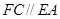 ,
,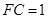 ,
,
 平面
平面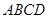 .
.
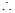
 与
与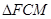 都是等腰直角三角形.
都是等腰直角三角形.
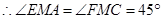 .
.
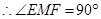 ,即
,即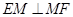 (也可由勾股定理证得).………………5分
(也可由勾股定理证得).………………5分
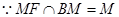 ,
, 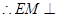 平面
平面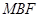 .
.
而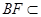 平面
平面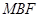 ,
,
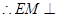
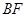 .
…………………………………………6分
.
…………………………………………6分
(Ⅱ)延长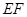 交
交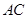 于
于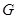 ,连
,连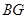 ,过
,过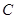 作
作 ,连结
,连结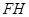 .
.
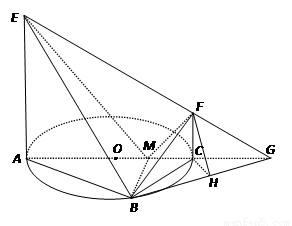
由(1)知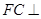 平面
平面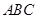 ,
,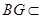 平面
平面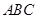 ,
,
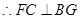 .
.
而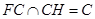 ,
, 平面
平面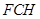 .
.
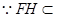 平面
平面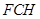 ,
,
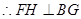 ,
,
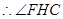 为平面
为平面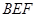 与平面
与平面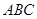 所成的
所成的
二面角的平面角. ……………………8分
在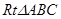 中,
中,
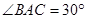 ,
,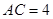 ,
,
 .
.
由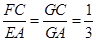 ,得
,得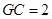 .
.
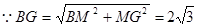 .
.
又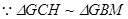 ,
,
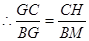 ,则
,则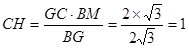 . ………………11分
. ………………11分
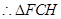 是等腰直角三角形,
是等腰直角三角形,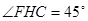 .
.
 平面
平面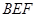 与平面
与平面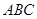 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为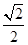 .
………………12分
.
………………12分

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目