题目内容
(本小题满分12分)
在![]() 中,
中,![]() ,AB的垂直平分线分别交AB,AC于D、E(图一),沿DE将
,AB的垂直平分线分别交AB,AC于D、E(图一),沿DE将![]() 折起,使得平面
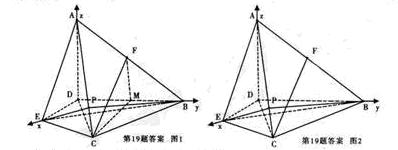
折起,使得平面![]() 平面BDEC(图二)。
平面BDEC(图二)。
(1)若F是AB的中点,求证:CF//平面ADE;
(2)P是AC上任意一点,求证:平面ACD![]() 平面PBE;
平面PBE;
(3)P是AC上一点,且AC![]() 平面PBE,求二面角P—BE—C的大小。
平面PBE,求二面角P—BE—C的大小。
略
解析:
(1)取BD的中点为M,连续FM,CM
![]() 为AB的中点,
为AB的中点,![]() MF//AD,
MF//AD,
由题知![]() 为等边三角形,
为等边三角形,
![]() BD,又DE
BD,又DE![]() BD
BD ![]() 2分
2分
![]() 面CFM//面ADE,
面CFM//面ADE,
![]() 面CMF,CF//面ADE 4分[来源:学+科+网]
面CMF,CF//面ADE 4分[来源:学+科+网]
(2)由平面几何知识:BE![]() CD,AD
CD,AD![]() DE,平面ADE
DE,平面ADE![]()
![]() 平面BDEC 5分
平面BDEC 5分
![]() 平面BDEC,
平面BDEC,
![]() 面ACD
面ACD
![]() 面PBE,
面PBE,![]() 平面ACD
平面ACD![]() 平面PBE 8分
平面PBE 8分
(3)法一,由(2)BE![]() 面ACD,
面ACD,
设![]() ,
,
由题意知BE![]() CD,BE
CD,BE![]() PQ,
PQ,
![]() PQC为二面角P—BE—C的平面角 10分
PQC为二面角P—BE—C的平面角 10分
AD=CD,![]()
![]()
![]() 二面角P—BE—C的大小为45° 12分
二面角P—BE—C的大小为45° 12分
(法二)
建立空间直角坐标系{DE、DB、DA},A(0,0,1),
则![]() 9分
9分
![]()
![]() 面PBE,AD
面PBE,AD![]() 面BCED
面BCED
设二面角P—BE—C的大小为![]() ,
,
则![]() 11分
11分
![]() 二面角P—BE—C的大小为45° 12分
二面角P—BE—C的大小为45° 12分

练习册系列答案
相关题目