题目内容
已知等差数列{an}满足:a5=9,a2+a6=14.(1)求{an}的通项公式;
(2)若
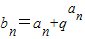 (q>0),求数列{bn}的前n项和Sn.
(q>0),求数列{bn}的前n项和Sn.
【答案】分析:(1)利用等差数列的通项公式与等差数列的性质即可求得{an}的通项公式;
(2)利用分组求和法即可求得数列{bn}的前n项和Sn.
解答:解:(1)∵在等差数列{an}中,a5=9,a2+a6=2a4=14,
∴a4=7,其公差d=a5-a4=2,
∴an=a4+(n-4)d=7+2(n-4)=2n-1.
(2)∵bn=an+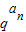 (q>0),
(q>0),
∴Sn=b1+b2+…+bn
=(a1+a2+…+an)+(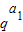 +
+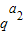 +…+
+…+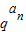 )
)
=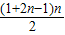 +(q1+q3+…+q2n-1)
+(q1+q3+…+q2n-1)
若q=1,Sn=n2+n;
若q≠1,Sn=n2+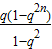 .
.
点评:本题考查等差数列的通项公式与数列求和,考查方程思想与转化思想的综合运用,属于中档题.
(2)利用分组求和法即可求得数列{bn}的前n项和Sn.
解答:解:(1)∵在等差数列{an}中,a5=9,a2+a6=2a4=14,
∴a4=7,其公差d=a5-a4=2,
∴an=a4+(n-4)d=7+2(n-4)=2n-1.
(2)∵bn=an+
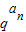 (q>0),
(q>0),∴Sn=b1+b2+…+bn
=(a1+a2+…+an)+(
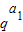 +
+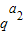 +…+
+…+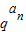 )
)=
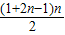 +(q1+q3+…+q2n-1)
+(q1+q3+…+q2n-1)若q=1,Sn=n2+n;
若q≠1,Sn=n2+
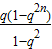 .
.点评:本题考查等差数列的通项公式与数列求和,考查方程思想与转化思想的综合运用,属于中档题.

练习册系列答案
相关题目
 已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.
已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.