Question

抛物线y=b（

x

a

）²、x轴及直线AB：x=a围成了如图（1）的阴影部分，AB与x轴交于点A，把线段OA分成n等份，作以

a

n

为底的内接矩形如图（2），阴影部分的面积为S等于这些内接矩形面积之和当n→∞时的极限值，求S．

Answer 1

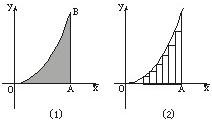
分析：首先分析题目把阴影部分分成n个小矩形，当n→∞时这些内接矩形面积之和的极限值为阴影部分面积，又已知内接矩形的底和高，故可以列出内接矩形的面积和，然后化简求得极限即可得到答案．

解答：解：因为把线段OA分成n等份，作以

a

n

为底的内接矩形，
所以S=

lim

n→∞

[b•（

1

n

）²+b•（

2

n

）²+b•（

3

n

）²++b•（

n-1

n

）²]²•

a

n

=

lim

n→∞

12+22++(n-1 ) 2

n3

•ab
=

lim

n→∞

(n-1)•n•(2n-1)

6n3

•ab
=

1

3

ab．

点评：此题主要考查极限及其运算问题，题目看似较复杂，但考查的都是基本的内容．求出内接矩形面积之和是解题的关键，有一定的计算量属于中档题目．