题目内容
试在抛物线y2=-4x上求一点P,使其到焦点F的距离与到A(-2,1)的距离之和最小,则该点坐标为
- A.

- B.
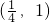
- C.

- D.

A
分析:先根据抛物线方程求出焦点坐标,再由抛物线的性质知:当P,A和焦点三点共线且点P在中间的时候距离之和最小,进而先求出纵坐标的值,代入到抛物线中可求得横坐标的值从而得到答案.
解答: 解:∵y2=-4x
解:∵y2=-4x
∴p=2,焦点坐标为(-1,0)
依题意可知当P,A和焦点三点共线且点P在中间的时候,距离之和最小如图,
故P的纵坐标为1,然后代入抛物线方程求得x=- ,
,
则该点坐标为:(- ,1).
,1).
故选A.
点评:本题主要考查了抛物线的定义,充分利用了抛物线上的点到准线的距离与点到焦点的距离相等这一特性,运用了转化思想和数形结合思想.
分析:先根据抛物线方程求出焦点坐标,再由抛物线的性质知:当P,A和焦点三点共线且点P在中间的时候距离之和最小,进而先求出纵坐标的值,代入到抛物线中可求得横坐标的值从而得到答案.
解答:
 解:∵y2=-4x
解:∵y2=-4x∴p=2,焦点坐标为(-1,0)
依题意可知当P,A和焦点三点共线且点P在中间的时候,距离之和最小如图,
故P的纵坐标为1,然后代入抛物线方程求得x=-
 ,
,则该点坐标为:(-
 ,1).
,1).故选A.
点评:本题主要考查了抛物线的定义,充分利用了抛物线上的点到准线的距离与点到焦点的距离相等这一特性,运用了转化思想和数形结合思想.

练习册系列答案
相关题目


