题目内容
已知数列{an}的各项均为正数，Sn为其前n项和，对于任意
，满足关系
.
（Ⅰ）证明：{an}是等比数列；
（Ⅱ）在正数数列{cn}中，设
，求数列{lncn}中的最大项.
（Ⅰ）证明：∵
①
∴
②
②－①，得
∵
故数列{an}是等比数列
（Ⅱ）解：据（Ⅰ）可知 
由
，得
令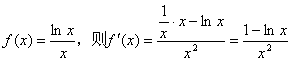
∵在区间（0，e）上，
∴在区间
为单调递减函数.
∴
是递减数列 又
∴数列
中的最大项为
练习册系列答案
相关题目
题目内容
已知数列{an}的各项均为正数，Sn为其前n项和，对于任意，满足关系.
（Ⅰ）证明：{an}是等比数列；
（Ⅱ）在正数数列{cn}中，设，求数列{lncn}中的最大项.
（Ⅰ）证明：∵ ①
∴ ②
②－①，得
∵
故数列{an}是等比数列
（Ⅱ）解：据（Ⅰ）可知
由，得
令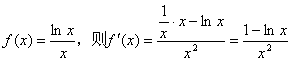
∵在区间（0，e）上，
∴在区间为单调递减函数.
∴是递减数列 又
∴数列中的最大项为
，则下列各数是否为数列中的项？如果是，是第几项？如果不是，为什么？（1）
（2）
，则下列各数是否为数列中的项？如果是，是第几项？如果不是，为什么？（1）
（2）