题目内容
已知函数f（x）=cosx•
+sinx•
（x∈（0.
）∪（
，π））（1）化简函数f（x）并求f（
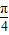）的值；（2）求函数f（x）在（
，π）上的单调区间和值域．
【答案】分析：（1）根据同角平方关系，分别在在被开方数上乘以1-sinx，1-cosx，根据已知的x的范围进行化简可得．
（2）结合（1）可得，f（x）=sinx-cosx=
，结合正弦函数的图象及性质进行求解．
解答：解：（1）
=
=
（3分）
=
（6分）
∴
（7分）
（2）当
时，f（x）=sinx-cosx=
（8分）
当
时，
故当
时，函数f（x）单调递增，
当
时，函数f（x）单调递减；（11分）函数的值域是（1，
）．（12分）
点评：本题主要考查了三角函数的平方关系的运用，考查了三角函数的值域及单调区间的求解，属于基础知识的简单综合．
（2）结合（1）可得，f（x）=sinx-cosx=
，结合正弦函数的图象及性质进行求解．解答：解：（1）
=
=
（3分）=
（6分）∴
（7分）（2）当
时，f（x）=sinx-cosx=（8分）当
时，故当时，函数f（x）单调递增，当
时，函数f（x）单调递减；（11分）函数的值域是（1，）．（12分）点评：本题主要考查了三角函数的平方关系的运用，考查了三角函数的值域及单调区间的求解，属于基础知识的简单综合．
练习册系列答案
相关题目
已知函数f（x）=
，则关于x的方程f2（x）+bf（x）+c=0有5个不同实数解的充要条件是（ ）
|
| A、b＜-2且c＞0 |
| B、b＞-2且c＜0 |
| C、b＜-2且c=0 |
| D、b≥-2且c=0 |
已知函数f（x）的图象如图所示，则函数的值域为（ ）