题目内容
18．点集{（x，y）|（|x|-1）2+y2=4}表示的图形是一条封闭的曲线，这条封闭曲线所围成的区域面积是（ ）| A． | $\frac{16π}{3}+2\sqrt{3}$ | B． | $\frac{16π}{3}+4\sqrt{3}$ | C． | $\frac{24π}{3}+2\sqrt{3}$ | D． | $\frac{24π}{3}+4\sqrt{3}$ |
分析 由曲线的方程可得，曲线关于两个坐标轴及原点都是对称的，故画出图象，结合图象求得围成的曲线的面积．
解答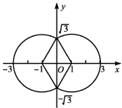 
解：点集{（x，y）|（|x|-1）2+y2=4}表示的图形是一条封闭的曲线，关于x，y轴对称，如图所示．
由图可得面积S=${S}_{菱形}+\frac{4}{3}{S}_{圆}$=$\frac{1}{2}×2\sqrt{3}×2$+$\frac{4}{3}×π×4$=$\frac{16π}{3}$+2$\sqrt{3}$．
故选：A．
点评 本题考查线段的方程特点，由曲线的方程研究曲线的对称性，体现了数形结合的数学思想．
练习册系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
8．如图所示，在“推理与证明”的知识结构图中，如果要加入“综合法”，则应该放在（ ）
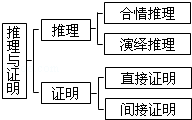
| A． | “合情推理”的下位 | B． | “直接证明”的下位 | ||
| C． | “演绎推理”的下位 | D． | “间接证明”的下位 |
9．已知等比数列{an}的前项和为Sn=2×（-1）n+a，n∈N*，则实数a的值是（ ）
| A． | -3 | B． | -2 | C． | -1 | D． | 0 |
6．已知F1，F2分别是中心在坐标原点，对称轴为做标轴的双曲线C的左、右焦点，过F2的直线l与双曲线的右支交于A，B两点，I1，I2分别为△AF1F2，△BF1F2的内心，若双曲线C的离心率为2，|I1I2|=$\frac{9}{2}$，直线l的倾斜角的正弦值为$\frac{8}{9}$，则双曲线C的方程为（ ）
| A． | x${\;}^{2}+\frac{{y}^{2}}{3}$=1 | B． | $\frac{{x}^{2}}{16}-\frac{{y}^{2}}{48}$=1 | C． | $\frac{{x}^{2}}{2}-\frac{{y}^{2}}{6}$=1 | D． | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1 |
10．已知函数f（x）=sin（ωx+$\frac{π}{6}$），其中ω＞0，若f（$\frac{π}{6}$）=f（$\frac{π}{3}$），且f（x）在区间（$\frac{π}{6}$，$\frac{π}{3}$）上有最小值、无最大值，则ω等于（ ）
| A． | $\frac{40}{3}$ | B． | $\frac{28}{3}$ | C． | $\frac{16}{3}$ | D． | $\frac{4}{3}$ |
