题目内容
在直角坐标系 中,曲线
中,曲线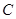 的参数方程为
的参数方程为 (
( 为参数),若以直角坐标系
为参数),若以直角坐标系 的
的 点为极点,
点为极点, 轴正方向为极轴,且长度单位相同,建立极坐标系,得直线
轴正方向为极轴,且长度单位相同,建立极坐标系,得直线 的极坐标方程为
的极坐标方程为 .求直线
.求直线 与曲线
与曲线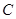 交点的极坐标.
交点的极坐标.

解析试题分析:求直线 与曲线
与曲线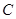 交点的极坐标,可先直线
交点的极坐标,可先直线 与曲线
与曲线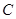 交点直角坐标..先根据
交点直角坐标..先根据 ,消去参数
,消去参数 得
得 ,注意范围:
,注意范围: .再根据
.再根据 得直线
得直线 的方程:
的方程: ,由
,由 , 解得
, 解得 . 所以交点的极坐标为
. 所以交点的极坐标为 .
.
直线 的直角坐标方程为
的直角坐标方程为 ,故直线
,故直线 的倾斜角为
的倾斜角为 .
.
曲线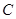 的普通方程为
的普通方程为
 ,
,
由 , 解得
, 解得 . 所以交点的极坐标为
. 所以交点的极坐标为 .
.
考点:参数方程化普通方程,极坐标方程化直角坐标方程

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
 中,以原点
中,以原点 为极点,
为极点, 轴的正半轴
轴的正半轴 的参数方程为
的参数方程为 (
( 为参数),曲线
为参数),曲线 的极坐标方程为
的极坐标方程为 ,则
,则 的参数方程为
的参数方程为 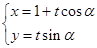 (t为参数,
(t为参数, 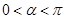 ),曲线C的极坐标方程为
),曲线C的极坐标方程为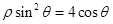 .
.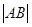 的最小值
的最小值 的参数方程为
的参数方程为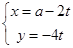 ,(
,(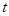 为参数),圆
为参数),圆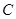 的参数方程为
的参数方程为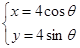 ,(
,(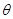 为常数).
为常数). 的取值范围.
的取值范围. (θ为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l的方程为ρsin
(θ为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l的方程为ρsin 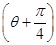 =2
=2 .
. 的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同,已知曲线
的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同,已知曲线 的极坐标方程为
的极坐标方程为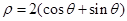 .
.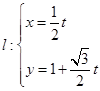 (
(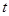 为参数)与曲线C交于
为参数)与曲线C交于 ,
, 两点,与
两点,与 轴交于
轴交于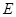 ,求
,求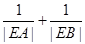 的值.
的值. 中,曲线
中,曲线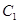 的参数方程为
的参数方程为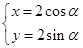 (
(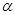 为参数).在极坐标系(与直角坐标系
为参数).在极坐标系(与直角坐标系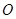 为极点,以
为极点,以 轴为极轴)中,曲线
轴为极轴)中,曲线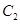 的方程
的方程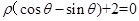 ,
,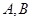 ,则公共弦
,则公共弦 的长是 .
的长是 . 的参数方程为
的参数方程为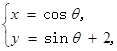
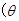 为参数), 以原点为极点,
为参数), 以原点为极点,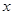 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线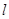 的极坐标方程为
的极坐标方程为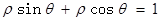 , 则直线
, 则直线 (θ为参数)交于点A、B,求PA·PB的值.
(θ为参数)交于点A、B,求PA·PB的值.