题目内容
若关于x的方程x2+（1+2i）x+3m+i=0有实根，则实数m等于（ ）A．
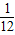
B．
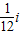
C．-
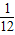
D．-
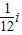
【答案】分析：若关于x的方程x2+（1+2i）x+3m+i=0有实根，由复数相等的概念可以得到关于实数x与实数m的方程，解出即可．
解答：解：若方程有实根，将方程x2+（1+2i）x+3m+i=0变为i（2x+1）+x2+x+3m=0，
由此得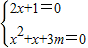
，
解得m=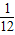
．
故选A．
点评：本题考查复数的相等等基本概念，求解本题关键是掌握好复数相等的充要条件，属于基础题．
解答：解：若方程有实根，将方程x2+（1+2i）x+3m+i=0变为i（2x+1）+x2+x+3m=0，
由此得
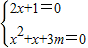，解得m=
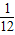．故选A．
点评：本题考查复数的相等等基本概念，求解本题关键是掌握好复数相等的充要条件，属于基础题．
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
△ABC中三个内角为A、B、C，若关于x的方程x2-xcosAcosB-cos2
=0有一根为1，则△ABC一定是（ ）
| C |
| 2 |
| A、直角三角形 |
| B、等腰三角形 |
| C、锐角三角形 |
| D、钝角三角形 |