题目内容
已知函数y=f(x)是定义在R上的奇函数,且满足f(x+2)=f(x),又当x∈(0,1)时,f(x)=2x-1,则f( )的值等于________.
)的值等于________.
-
分析:由题可先研究 的取值范围,利用函数的周期性与函数的奇函数的性质将f(
的取值范围,利用函数的周期性与函数的奇函数的性质将f( )的值用f(
)的值用f(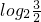 )的值表示出来,再由x∈(0,1)时,f(x)=2x-1,即可求出所求值.
)的值表示出来,再由x∈(0,1)时,f(x)=2x-1,即可求出所求值.
解答:由题意函数y=f(x)满足f(x+2)=f(x),可得其周期是2
又-3=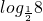 <
< <
<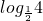 =-2
=-2
故-1<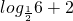 <0,即
<0,即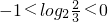 ,可得
,可得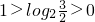
∴f( )=f(
)=f( +2)=f(
+2)=f(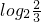 )
)
又函数y=f(x)是定义在R上的奇函数
∴f( )=f(
)=f(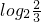 )=-f(
)=-f(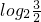 )=-
)=- +1=-
+1=-
故答案为:- .
.
点评:本题考点是函数奇函数的性质,考查了奇函数的对称性,函数的周期性,对数的去处性质,解题的关键是由函数的性质将f( )的值用f(
)的值用f(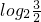 )的值表示出来,这是本题的难点,本题考察了转化的思想,本题是一个函数性质综合考查题,此类题是每年高考必考题,规律较固定,题后要好好总结.
)的值表示出来,这是本题的难点,本题考察了转化的思想,本题是一个函数性质综合考查题,此类题是每年高考必考题,规律较固定,题后要好好总结.

分析:由题可先研究
 的取值范围,利用函数的周期性与函数的奇函数的性质将f(
的取值范围,利用函数的周期性与函数的奇函数的性质将f( )的值用f(
)的值用f(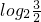 )的值表示出来,再由x∈(0,1)时,f(x)=2x-1,即可求出所求值.
)的值表示出来,再由x∈(0,1)时,f(x)=2x-1,即可求出所求值.解答:由题意函数y=f(x)满足f(x+2)=f(x),可得其周期是2
又-3=
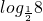 <
< <
<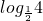 =-2
=-2故-1<
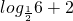 <0,即
<0,即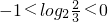 ,可得
,可得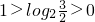
∴f(
 )=f(
)=f( +2)=f(
+2)=f(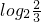 )
)又函数y=f(x)是定义在R上的奇函数
∴f(
 )=f(
)=f(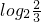 )=-f(
)=-f(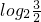 )=-
)=- +1=-
+1=-
故答案为:-
 .
.点评:本题考点是函数奇函数的性质,考查了奇函数的对称性,函数的周期性,对数的去处性质,解题的关键是由函数的性质将f(
 )的值用f(
)的值用f(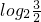 )的值表示出来,这是本题的难点,本题考察了转化的思想,本题是一个函数性质综合考查题,此类题是每年高考必考题,规律较固定,题后要好好总结.
)的值表示出来,这是本题的难点,本题考察了转化的思想,本题是一个函数性质综合考查题,此类题是每年高考必考题,规律较固定,题后要好好总结. 
练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案
相关题目
 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为 已知函数y=f(x)的图象如图,则满足
已知函数y=f(x)的图象如图,则满足