题目内容
将直线l1:nx+y-n=0和直线l2:x+ny-n=0(n∈N*,n≥2)x轴、y轴围成的封闭图形的面积记为Sn,则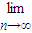 Sn= .
Sn= .
【答案】分析:联立两条直线方程求出交点B的坐标,因为两直线分别恒过定点,分别求出围成图形的两条对角线,由两条对角线垂直,利用四边形对角线垂直时面积为对角线乘积的一半表示出sn,求出极限即可.
解答:解:联立直线l1和直线l2 解得:x=y=
解得:x=y= ,所以得到B(
,所以得到B( ,
, );
);
观察可得直线l1过点A(1,0),直线l2过点C(0,1),
显然BO⊥AC,根据勾股定理得AC= ,BO=
,BO= •
• ,
,
所以两直线与x、y轴围成的封闭图形的面积记Sn= ×
× ×
×
 =
=
所以 Sn=
Sn=
 =1.
=1.
故答案为:1
点评:此题为一道综合题,要求学生会求两直线的交点坐标,会根据对角线垂直求任意四边形的面积,会进行极限的运算.
解答:解:联立直线l1和直线l2
 解得:x=y=
解得:x=y= ,所以得到B(
,所以得到B( ,
, );
);观察可得直线l1过点A(1,0),直线l2过点C(0,1),
显然BO⊥AC,根据勾股定理得AC=
 ,BO=
,BO= •
• ,
,所以两直线与x、y轴围成的封闭图形的面积记Sn=
 ×
× ×
×
 =
=
所以
 Sn=
Sn=
 =1.
=1.故答案为:1
点评:此题为一道综合题,要求学生会求两直线的交点坐标,会根据对角线垂直求任意四边形的面积,会进行极限的运算.

练习册系列答案
相关题目
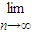 Sn= .
Sn= . ( )。
( )。