题目内容
甲、乙两台机床在相同的技术条件下,同时生产一种零件,现在从中抽测10个,它们的尺寸分别如下(单位:mm).
甲机床:10.2 10.1 10 9.8 9.9 10.3 9.7 10 9.9 10.1;
乙机床:10.3 10.4 9.6 9.9 10.1 10.9 8.9 9.7 10.2 10.
分别计算上面两个样本的平均数和方差.如图纸规定零件的尺寸为10 mm,从计算的结果来看哪台机床加工这种零件较合适?(要求利用公式笔算)
解:![]() 甲=
甲=![]() =
=![]()
![]() 乙=
乙=![]()
∴s甲2=![]() [(10.2-10)2+(10.1-10)2+…+(10.1-10)2]
[(10.2-10)2+(10.1-10)2+…+(10.1-10)2]
=![]() (0.22+0.12+0+0.22+0.12+0.32+0.32+0+0.12+0.12)
(0.22+0.12+0+0.22+0.12+0.32+0.32+0+0.12+0.12)
=![]() (0.04+0.01+0+0.04+0.01+0.09+0.09+0+0.01+0.01)
(0.04+0.01+0+0.04+0.01+0.09+0.09+0+0.01+0.01)
=![]() ×0.3=0.03(mm2)
×0.3=0.03(mm2)
s乙2=![]() [(10.3-10)2+(10.4-10)2+…+(10-10)2]
[(10.3-10)2+(10.4-10)2+…+(10-10)2]
=![]() (0.32+0.42+0.42+0.12+0.12+0+0.22+0.32+0.22+0)
(0.32+0.42+0.42+0.12+0.12+0+0.22+0.32+0.22+0)
=![]() (0.09+0.16+0.16+0.01+0.01+0.04+0.09+0.04)
(0.09+0.16+0.16+0.01+0.01+0.04+0.09+0.04)
=![]() ×0.6=0.06 (mm2)
×0.6=0.06 (mm2)
∴s甲2<s乙2
∴用甲机床比乙机床稳定,即用甲机床加工较合适.
注意:此题两机床生产零件尺寸的平均数相等都是10 mm,与规定尺寸相同,但方差不同,从方差可以估计出哪个机床加工的零件较合适。

练习册系列答案
相关题目
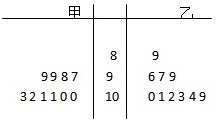 甲、乙两台机床在相同的技术条件下,同时生产一种零件,现在从中抽测10个,它们的尺寸用茎叶图表示如图,中间一列的数字表示零件尺寸的十位数(第三行是十位及百位,如甲,第三行对应零件尺寸为103,102,101,101…),两边的数字表示零件个数的个位数
甲、乙两台机床在相同的技术条件下,同时生产一种零件,现在从中抽测10个,它们的尺寸用茎叶图表示如图,中间一列的数字表示零件尺寸的十位数(第三行是十位及百位,如甲,第三行对应零件尺寸为103,102,101,101…),两边的数字表示零件个数的个位数