题目内容
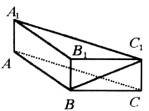
如图，A1B1C1－ABC是直三棱柱，过点A1、B1、C1的平面和平面ABC的交线记作l．
(1)判定直线A1C1和l的位置关系，并加以证明；
(2)若A1A=1，AB=4，BC=3，∠ABC=90°，求顶点A1到直线l的距离．
答案：
解析：
解析：
(1) 如图，因而ABC∥面A1B1C1，又过A1、B、C1的平面与这两平面都相交， 故知这两交线平行，而A1C1是面A1BC1与面A1B1C1的交线且A1C1∥AC， 所以只须在面ABC内过B作AC的平行线，即为所求作的l，且l∥A1C1．
(2)过A作AD⊥l于D，连A1D，则A1D⊥l， ∴A1D即为所求，在Rt△A1AD中，易求得A1D= |
．
练习册系列答案
相关题目
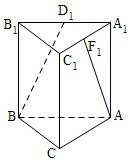如图，A1B1C1-ABC是直三棱柱，∠BCA=90°，点D1、F1分别是A1B1、A1C1的中点，若BC=CA=CC1，则BD1与AF1所成角的余弦值是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
9、如图，A1B1C1为正三角形，与平面不平行，且CC1＞BB1＞AA1，则多面体的正视图（也称主视图）是（ ）
B．
C．
D．
B．
D．
B．
C．
D．