题目内容
22.已知函数f(x)=e-x(cosx+sinx),将满足f′(x)=0的所有正数x从小到大排成数列{xn}.(Ⅰ)证明数列{f(xn)}为等比数列;
(Ⅱ)记Sn是数列{xnf(xn)}的前n项和,求![]()
![]() .
.
22.本小题主要考查函数的导数,三角函数的性质,等差数列与等比数列的概念和性质,以及综合运用的能力.
(Ⅰ)证明:f′(x)=-e-x(cosx+sinx)+e-x(-sinx+cosx)=-2e-xsinx,
由f′(x)=0,即-2e-xsinx=0,
解得x=n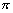 ,n为整数.从而xn=n
,n为整数.从而xn=n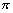 ,n=1,2,3…
,n=1,2,3…
f(xn)=(-1)n![]() .
.
![]() =-e-π.
=-e-π.
所以数列{f(xn)}是公比q=-![]() 的等比数列,且首项f(x1)=q.
的等比数列,且首项f(x1)=q.
(Ⅱ)解:Sn=x1f(x1)+x2f(x2)+…+xnf(xn)
=πq(1+2q+…+nqn-1),
qSn=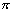 q(q+2q2+…+nqn),
q(q+2q2+…+nqn),
Sn-qSn=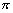 q(1+q+…+qn-1-nqn)
q(1+q+…+qn-1-nqn)
=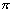 q(
q(![]() -nqn),
-nqn),
从而Sn=![]() (
(![]() -nqn).
-nqn).
![]()
=![]() -
-![]() (1+q+…+qn-1)-
(1+q+…+qn-1)-![]() (1+2q+…+nqn-1)
(1+2q+…+nqn-1)
=![]() -
-![]()
![]() -
-![]() (
(![]() -nqn)
-nqn)
=![]() -
-![]() (1-qn)+
(1-qn)+![]() .
.
因为|![]() |=e-x<1,
|=e-x<1,![]()
![]() n=0,所以
n=0,所以
![]()
![]() =
=![]() =
=![]() .
.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目