题目内容
(本小题满分16分)
已知函数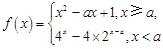
(1) 若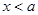 时,
时,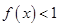 恒成立,求
恒成立,求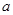 的取值范围;
的取值范围;
(2) 若 时,函数
时,函数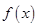 在实数集
在实数集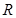 上有最小值,求实数
上有最小值,求实数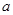 的取值范围.
的取值范围.
已知函数
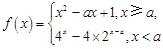
(1) 若
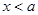 时,
时,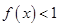 恒成立,求
恒成立,求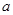 的取值范围;
的取值范围;(2) 若
 时,函数
时,函数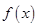 在实数集
在实数集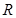 上有最小值,求实数
上有最小值,求实数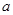 的取值范围.
的取值范围.(1) 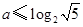 .
.
(2)当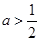 时,函数
时,函数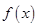 有最小值为
有最小值为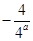 ;当
;当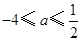 时,函数
时,函数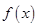 无最小值.
无最小值.
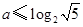 .
. (2)当
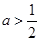 时,函数
时,函数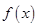 有最小值为
有最小值为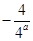 ;当
;当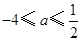 时,函数
时,函数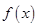 无最小值.
无最小值.本试题主要是考查了分段函数的最值和函数与不等式的关系的综合运用。
(1)因为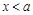 时,
时,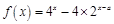 ,所以令
,所以令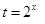 ,则有
,则有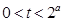 ,
,
 当
当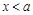 时恒成立,转化为
时恒成立,转化为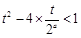 ,即
,即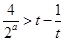 在
在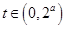 上恒成立利用分离参数的思想得到范围。
上恒成立利用分离参数的思想得到范围。
(2)当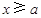 时,
时,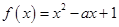 ,即
,即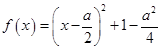 ,
,
对于二次函数要讨论对称轴与定义域的关系得到最值。
(1) 因为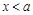 时,
时,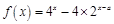 ,所以令
,所以令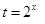 ,则有
,则有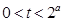 ,
,
 当
当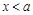 时恒成立,转化为
时恒成立,转化为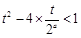 ,即
,即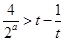 在
在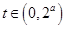 上恒成立,………2分
上恒成立,………2分
令p (t)=t-,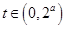 ,则
,则 ,所以p (t)=t-在
,所以p (t)=t-在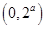 上单调递增,
上单调递增,
所以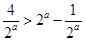 ,所以
,所以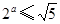 ,解得
,解得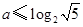 . ……………………………………6分
. ……………………………………6分
(2) 当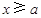 时,
时,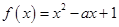 ,即
,即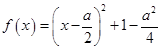 ,
,
当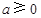 时,即
时,即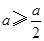 ,
,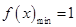 ;
;
当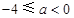 时,即
时,即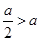 ,
,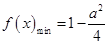 .……………………………………………9分
.……………………………………………9分
当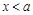 时,
时,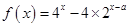 ,令
,令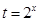 ,
,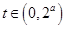 ,则
,则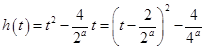 ,
,
当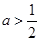 时,即
时,即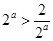 ,
,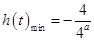 ;
;
当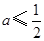 时,即
时,即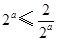 ,
,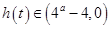 ,此时
,此时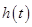 无最小值;……………………12分
无最小值;……………………12分
所以,当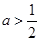 时,即
时,即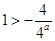 ,函数
,函数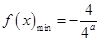 ;
;
当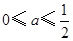 时,
时, 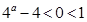 ,函数
,函数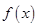 无最小值;
无最小值;
当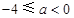 时,
时, 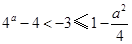 ,函数
,函数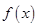 无最小值.…………………………15分
无最小值.…………………………15分
综上所述,当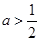 时,函数
时,函数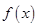 有最小值为
有最小值为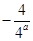 ;当
;当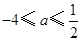 时,函数
时,函数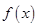 无最小值.
无最小值.
(1)因为
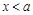 时,
时,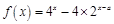 ,所以令
,所以令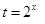 ,则有
,则有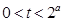 ,
, 当
当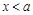 时恒成立,转化为
时恒成立,转化为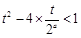 ,即
,即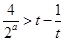 在
在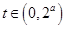 上恒成立利用分离参数的思想得到范围。
上恒成立利用分离参数的思想得到范围。(2)当
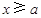 时,
时,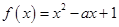 ,即
,即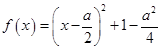 ,
,对于二次函数要讨论对称轴与定义域的关系得到最值。
(1) 因为
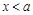 时,
时,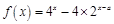 ,所以令
,所以令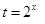 ,则有
,则有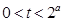 ,
, 当
当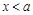 时恒成立,转化为
时恒成立,转化为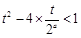 ,即
,即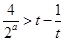 在
在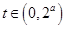 上恒成立,………2分
上恒成立,………2分令p (t)=t-,
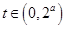 ,则
,则 ,所以p (t)=t-在
,所以p (t)=t-在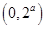 上单调递增,
上单调递增,所以
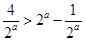 ,所以
,所以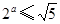 ,解得
,解得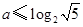 . ……………………………………6分
. ……………………………………6分(2) 当
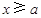 时,
时,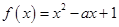 ,即
,即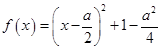 ,
,当
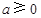 时,即
时,即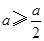 ,
,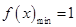 ;
;当
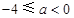 时,即
时,即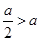 ,
,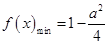 .……………………………………………9分
.……………………………………………9分当
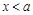 时,
时,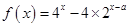 ,令
,令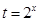 ,
,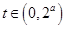 ,则
,则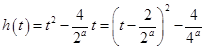 ,
,当
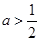 时,即
时,即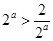 ,
,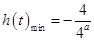 ;
;当
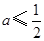 时,即
时,即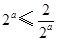 ,
,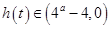 ,此时
,此时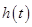 无最小值;……………………12分
无最小值;……………………12分所以,当
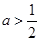 时,即
时,即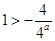 ,函数
,函数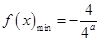 ;
;当
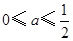 时,
时, 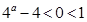 ,函数
,函数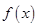 无最小值;
无最小值;当
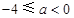 时,
时, 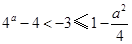 ,函数
,函数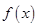 无最小值.…………………………15分
无最小值.…………………………15分综上所述,当
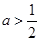 时,函数
时,函数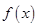 有最小值为
有最小值为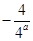 ;当
;当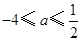 时,函数
时,函数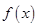 无最小值.
无最小值.
练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
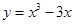 的极大值。
的极大值。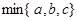 表示a、b、c这三个数中的最小值。设
表示a、b、c这三个数中的最小值。设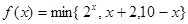
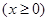 ,则f(x)的最大值为( )
,则f(x)的最大值为( )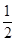 <x≤m+
<x≤m+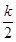 (k∈Z)对称;
(k∈Z)对称;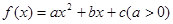 ,满足
,满足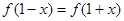 ,则
,则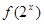 与
与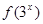 的大小关系
的大小关系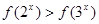
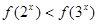
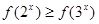
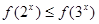
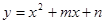 有两个不同的零点
有两个不同的零点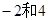 ,则
,则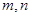 的值是
的值是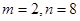
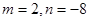
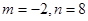
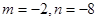
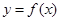 是偶函数,当
是偶函数,当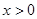 时,
时,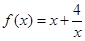 ,且当
,且当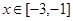 时,
时,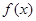 的值域是
的值域是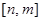 ,则
,则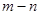 的值是 ( )
的值是 ( )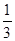
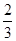
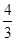
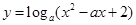 在区间
在区间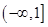 上为减函数,则a的取值范围是
上为减函数,则a的取值范围是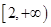
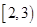

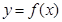 是奇函数,当
是奇函数,当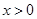 时,
时,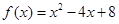 ,且当
,且当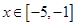 时,
时,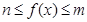 恒成立,则
恒成立,则 的最小值为 .
的最小值为 .