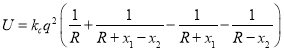题目内容
【题目】在平面直角坐标系![]() 中,设椭圆
中,设椭圆![]() (
(![]() )的离心率是e,定义直线
)的离心率是e,定义直线![]() 为椭圆的“类准线”,已知椭圆C的“类准线”方程为
为椭圆的“类准线”,已知椭圆C的“类准线”方程为![]() ,长轴长为4.
,长轴长为4.
(1)求椭圆C的方程;
(2)点P在椭圆C的“类准线”上(但不在y轴上),过点P作圆O:![]() 的切线l,过点O且垂直于
的切线l,过点O且垂直于![]() 的直线l交于点A,问点A是否在椭圆C上?证明你的结论.
的直线l交于点A,问点A是否在椭圆C上?证明你的结论.
【答案】(1)![]() ;(2)在,证明见解析.
;(2)在,证明见解析.
【解析】
(1)由题意列关于a,b,c的方程,联立方程组求得![]() ,
,![]() ,
,![]() ,则椭圆方程可求;
,则椭圆方程可求;
(2)设![]() (
(![]() ),当
),当![]() 时和
时和![]() 时,求出A的坐标,代入椭圆方程验证知,A在椭圆上,当
时,求出A的坐标,代入椭圆方程验证知,A在椭圆上,当![]() 时,求出过点O且垂直于
时,求出过点O且垂直于![]() 的直线与椭圆的交点,写出该交点与P点的连线所在直线方程,由原点到直线的距离等于圆的半径说明直线是圆的切线,从而说明点A在椭圆C上.
的直线与椭圆的交点,写出该交点与P点的连线所在直线方程,由原点到直线的距离等于圆的半径说明直线是圆的切线,从而说明点A在椭圆C上.
(1)由题意得:![]() ,
,![]() ,又
,又![]() ,
,
联立以上可得:![]() ,
,![]() ,
,![]() .∴椭圆C的方程为
.∴椭圆C的方程为![]() ;
;
(2)如图,由(1)可知,椭圆的类准线方程为![]() ,不妨取
,不妨取![]() ,
,
设![]() (
(![]() ),则
),则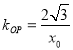 ,
,
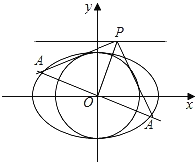
∴过原点且与![]() 垂直的直线方程为
垂直的直线方程为![]() ,
,
当![]() 时,过P点的圆的切线方程为
时,过P点的圆的切线方程为![]() ,
,
过原点且与![]() 垂直的直线方程为
垂直的直线方程为![]() ,联立
,联立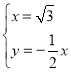 ,解得:
,解得: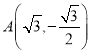 ,
,
代入椭圆方程成立;
同理可得,当![]() 时,点A在椭圆上;
时,点A在椭圆上;
当![]() 时,联立
时,联立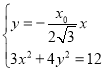 ,
,
解得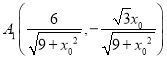 ,
,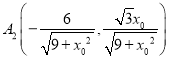 ,
,
![]() 所在直线方程为
所在直线方程为![]() .
.
此时原点O到该直线的距离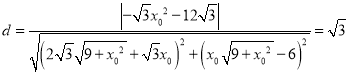 ,
,
∴说明A点在椭圆C上;同理说明另一种情况的A也在椭圆C上.
综上可得,点A在椭圆C上.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费对年销售量(单位:![]() )的影响.该公司对近5年的年宣传费和年销售量数据进行了研究,发现年宣传费
)的影响.该公司对近5年的年宣传费和年销售量数据进行了研究,发现年宣传费![]() (万元)和年销售量
(万元)和年销售量![]() (单位:
(单位:![]() )具有线性相关关系,并对数据作了初步处理,得到下面的一些统计量的值.
)具有线性相关关系,并对数据作了初步处理,得到下面的一些统计量的值.
| 2 | 4 | 5 | 3 | 6 |
| 2.5 | 4 | 4.5 | 3 | 6 |
(1)根据表中数据建立年销售量![]() 关于年宣传费
关于年宣传费![]() 的回归方程;
的回归方程;
(2)已知这种产品的年利润![]() 与
与![]() ,
,![]() 的关系为
的关系为![]() ,根据(1)中的结果回答下列问题:
,根据(1)中的结果回答下列问题:
①当年宣传费为10万元时,年销售量及年利润的预报值是多少?
②估算该公司应该投入多少宣传费,才能使得年利润与年宣传费的比值最大.
附:问归方程![]() 中的斜率和截距的最小二乘估计公式分别为
中的斜率和截距的最小二乘估计公式分别为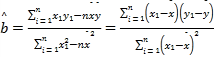 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.