题目内容
已知函数f(x)=sinxcosx+sin2x.
(Ⅰ)求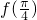 的值;
的值;
(II)若 ,求f(x)的最大值及相应的x值.
,求f(x)的最大值及相应的x值.
解:(Ⅰ)∵f(x)=sinxcosx+sin2x,
∴ ,…(1分)
,…(1分)
= …(4分)
…(4分)
=1.…(6分)
(Ⅱ)f(x)=sinxcosx+sin2x= ,…(8分)
,…(8分)
= =
= ,…(9分)
,…(9分)
由 得
得 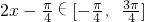 ,…(11分)
,…(11分)
所以,当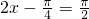 ,即
,即 时,f(x)取到最大值为
时,f(x)取到最大值为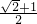 .…(13分)
.…(13分)
分析:(Ⅰ)把x= 代入函数的解析式,化简求得结果.
代入函数的解析式,化简求得结果.
(Ⅱ)利用三角函数的恒等变换化简f(x)的解析式为 ,由x的范围,得
,由x的范围,得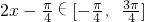 ,
,
故当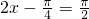 ,即
,即 时,f(x)取到最大值.
时,f(x)取到最大值.
点评:本题主要考查三角函数的恒等变换及化简求值,正弦函数的定义域和值域,属于基础题.
∴
 ,…(1分)
,…(1分)=
 …(4分)
…(4分)=1.…(6分)
(Ⅱ)f(x)=sinxcosx+sin2x=
 ,…(8分)
,…(8分)=
 =
= ,…(9分)
,…(9分)由
 得
得 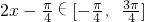 ,…(11分)
,…(11分)所以,当
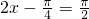 ,即
,即 时,f(x)取到最大值为
时,f(x)取到最大值为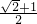 .…(13分)
.…(13分)分析:(Ⅰ)把x=
 代入函数的解析式,化简求得结果.
代入函数的解析式,化简求得结果.(Ⅱ)利用三角函数的恒等变换化简f(x)的解析式为
 ,由x的范围,得
,由x的范围,得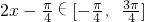 ,
,故当
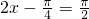 ,即
,即 时,f(x)取到最大值.
时,f(x)取到最大值.点评:本题主要考查三角函数的恒等变换及化简求值,正弦函数的定义域和值域,属于基础题.

练习册系列答案
相关题目
