题目内容
设甲、乙两楼相距20m，从乙楼底望甲楼顶的仰角为60°，从甲楼顶望乙楼顶的俯角为30°，则甲、乙两楼的高分别是（ ）
A．20
| B．10
| ||||||||||||||
C．10（
| D．
|
过点B作BE⊥AE于点E，
∴∠E=90°，
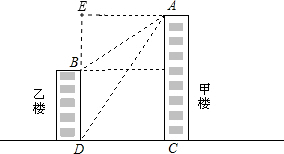
根据题意得：CD=AE=20米，∠EAB=30°，∠ADC=60°，
在Rt△ABE中，tan∠EAB=tan30°=
=
∴BE=
AE=20×
=
（米），
在Rt△ACD中，tan∠ADC=tan60°=
∴AC=CD•tan60°=20
（米），
BD=AC-BE=20
-
=
（米）
故选A
∴∠E=90°，
根据题意得：CD=AE=20米，∠EAB=30°，∠ADC=60°，
在Rt△ABE中，tan∠EAB=tan30°=
| BE |
| AE |
| ||
| 3 |
∴BE=
| ||
| 3 |
| ||
| 3 |
20
| ||
| 3 |
在Rt△ACD中，tan∠ADC=tan60°=
| AC |
| CD |
∴AC=CD•tan60°=20
| 3 |
BD=AC-BE=20
| 3 |
20
| ||
| 3 |
40
| ||
| 3 |
故选A
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
m，
m
m，20
m
-
） m，20
m
m，
m
m，
m
m，20
m
-
） m，20
m
m，
m