题目内容
已知函数f(x)=lnx,g(x)=x.
(Ⅰ)若x>1,求证: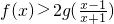 ;
;
(Ⅱ)求实数k的取值范围,使得方程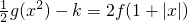 有四个不同的实数根.
有四个不同的实数根.
解:(Ⅰ)令 =
= ,
, .
.
当x>1时,F'(x)>0 恒成立,∴F(x)在(1,+∞)上是增函数.
∵F(x)在x=1 处连续,∴F(x)>F(1).
∵F(1)=0,∴当x∈(1,+∞)时,F(x)>0 恒成立.
∴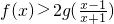 .
.
(Ⅱ)原方程化为 ,
,
令 ,则
,则 .
.
∵G(-x)=G(x),∴G(x)是偶函数.
当x≥0时, (x≥0),
(x≥0),
则 =
= .
.
∵x≥0,∴令G'(x)=0,得x=1.
当x∈[0,1),G'(x)<0,G(x)单调递减;
当x∈(1,+∞),G'(x)>0,G(x)单调递增.
∴x≥0时,在x=1处G(x)取得极小值为G(1)= .
.
又G(0)=0,∴当k∈( ,0)时函数
,0)时函数 (x≥0)与y=k 有两个不同的交点.
(x≥0)与y=k 有两个不同的交点.
∵G(x)是偶函数,
∴G(x)=k在k∈( ,0)时有四个不同的实数根.
,0)时有四个不同的实数根.
分析:(Ⅰ)先令 =
= ,求导数得到
,求导数得到 .
.
利用导数的性质得出F(x)在(1,+∞)上是增函数.F(x)>F(1).从而证得结论;
(Ⅱ)原方程化为 ,令
,令 ,则
,则 .
.
利用导数研究其单调性即可解决问题.
点评:本小题主要考查利用导数研究函数的单调性、利用导数研究函数的极值等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.
 =
= ,
, .
.当x>1时,F'(x)>0 恒成立,∴F(x)在(1,+∞)上是增函数.
∵F(x)在x=1 处连续,∴F(x)>F(1).
∵F(1)=0,∴当x∈(1,+∞)时,F(x)>0 恒成立.
∴
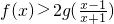 .
.(Ⅱ)原方程化为
 ,
,令
 ,则
,则 .
.∵G(-x)=G(x),∴G(x)是偶函数.
当x≥0时,
 (x≥0),
(x≥0),则
 =
= .
.∵x≥0,∴令G'(x)=0,得x=1.
当x∈[0,1),G'(x)<0,G(x)单调递减;
当x∈(1,+∞),G'(x)>0,G(x)单调递增.
∴x≥0时,在x=1处G(x)取得极小值为G(1)=
 .
.又G(0)=0,∴当k∈(
 ,0)时函数
,0)时函数 (x≥0)与y=k 有两个不同的交点.
(x≥0)与y=k 有两个不同的交点.∵G(x)是偶函数,
∴G(x)=k在k∈(
 ,0)时有四个不同的实数根.
,0)时有四个不同的实数根.分析:(Ⅰ)先令
 =
= ,求导数得到
,求导数得到 .
.利用导数的性质得出F(x)在(1,+∞)上是增函数.F(x)>F(1).从而证得结论;
(Ⅱ)原方程化为
 ,令
,令 ,则
,则 .
.利用导数研究其单调性即可解决问题.
点评:本小题主要考查利用导数研究函数的单调性、利用导数研究函数的极值等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目