题目内容
如果△A1BA.△A1B
B.△A1B
C.△A1B
D.△A1B
分析:本题使用特殊值法.
解法一:设△A2B
解法二:△A1B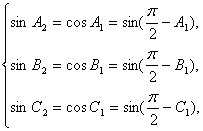 得
得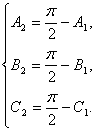
那么A2+B2+C2=![]() .所以△A2B
.所以△A2B
答案:D

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如果△A1B1C1的三个内角的余弦值分别等于△A2B2C2的三个内角的正弦值,则( )
| A、△A1B1C1和△A2B2C2都是锐角三角形 | B、△A1B1C1和△A2B2C2都是钝角三角形 | C、△A1B1C1是钝角三角形,△A2B2C2是锐角三角形 | D、△A1B1C1是锐角三角形,△A2B2C2是钝角三角形 |