题目内容
18.在锐角△ABC中,角A,B,C所对的边分别为a,b,c,若b=2,B=$\frac{π}{3}$且sin2A+sin(A+C)=sinB,则△ABC的面积为$\frac{2\sqrt{3}}{3}$.分析 由已知化简可得sin2A=0,即A=90°,从而可求C,由正弦定理可得c,利用三角形面积公式即可得解.
解答 解:∵锐角△ABC中,sin2A+sin(A+C)=sinB,
∴2sinAcosA=sin(A+C)-sin(A+C),
∴sin2A=0,即A=90°.
再由b=2,B=$\frac{π}{3}$ 可得C=$\frac{π}{6}$,
故由正弦定理可得:c=$\frac{bsinC}{sinB}$=$\frac{2×sin\frac{π}{6}}{sin\frac{π}{3}}$=$\frac{2\sqrt{3}}{3}$
∴△ABC的面积为:$\frac{1}{2}$×2×$\frac{2\sqrt{3}}{3}$=$\frac{2\sqrt{3}}{3}$.
故答案为:$\frac{2\sqrt{3}}{3}$.
点评 本题主要考查了正弦定理,三角形面积公式的应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.f(x)=x3+ax2+bx+c在区间(1,2)上有三个零点,则( )
| A. | f(1)f(2)≤$\frac{1}{64}$ | B. | f(1)f(2)<$\frac{1}{64}$ | C. | f(1)f(2)>-$\frac{1}{64}$ | D. | f(1)f(2)≥-$\frac{1}{64}$ |
3.函数f(x)=log2(1-3x)的定义域是( )
| A. | (0,+∞) | B. | [0,+∞) | C. | (-∞,0) | D. | (-∞,0] |
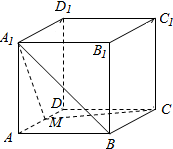 如图,在长方体ABCD-A1B1C1D1中,已知AB=AA1=a,BC=$\sqrt{2}$a,M是AD的中点.
如图,在长方体ABCD-A1B1C1D1中,已知AB=AA1=a,BC=$\sqrt{2}$a,M是AD的中点.