Question

4．已知函数f（x）=$\frac{x}{1+{x}^{2}}$．
（I）讨论函数f（x）的奇偶性；
（Ⅱ）作出函数f（x）的图象；
（Ⅲ）求函数f（x）的最大值与最小值．

Answer 1

分析 （I）根据函数奇偶性的定义即可讨论函数f（x）的奇偶性；
（Ⅱ）求函数的导数，判断函数的单调性和极值，即可作出函数f（x）的图象；
（Ⅲ）根据函数的图象即可求函数f（x）的最大值与最小值．

解答 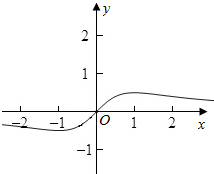解：（I）函数的定义域为（-∞，+∞），
则f（-x）=$\frac{-x}{1+{x}^{2}}$=-$\frac{x}{1+{x}^{2}}$=-f（x），
则函数f（x）为奇函数；
（Ⅱ）函数的导数f′（x）=$\frac{1+{x}^{2}-2{x}^{2}}{（1+{x}^{2}）^{2}}$=$\frac{1-{x}^{2}}{（1+{x}^{2}）^{2}}$，
由f′（x）＞0得-1＜x＜1，此时函数单调递增，
由f′（x）＜0得x＞1或x＜-1，此时函数单调递减，
即当x=1时，函数取得极大值为f（1）=$\frac{1}{2}$，
当x=-1时，函数取得极小值为f（-1）=-$\frac{1}{2}$，
则作出函数f（x）的图象；
（Ⅲ）由图象知，当x=1时，函数取得最大值为f（1）=$\frac{1}{2}$，
当x=-1时，函数取得最小值为f（-1）=-$\frac{1}{2}$．

点评 本题主要考查函数奇偶性和单调性，最值的判断和求解，考查函数的性质．