题目内容
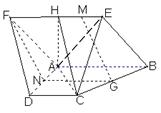
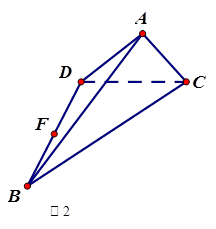
如图已知:菱形 所在平面与直角梯形ABCD所在平面互相垂直,
所在平面与直角梯形ABCD所在平面互相垂直, ,
, 点
点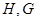 分别是线段
分别是线段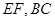 的中点.
的中点. 
(1)求证:平面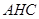
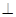 平面
平面 ;
;
(2)试问在线段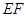 上是否存在点
上是否存在点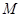 ,使得
,使得
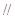 平面
平面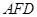 ,若存在,求
,若存在,求 的长并证明;若不存在,说明理由.
的长并证明;若不存在,说明理由.
(1)证明详见解析;(2)存在,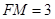 .
.
解析试题分析:(1)先证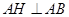 ,由面面垂直的性质定理得到
,由面面垂直的性质定理得到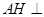 平面
平面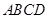 ,所以
,所以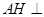
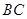 ,由勾股定理证
,由勾股定理证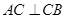 ,所以由线面垂直的判定定理得
,所以由线面垂直的判定定理得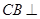 平面
平面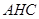 ,所以面面垂直的判定定理得平面
,所以面面垂直的判定定理得平面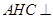 平面
平面 ;(2)先证四边形
;(2)先证四边形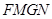 是平行四边形,得
是平行四边形,得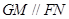 ,由线面平行的判定定理得
,由线面平行的判定定理得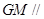 平面
平面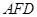 .
.
试题解析:(1)证明:在菱形 中,因为
中,因为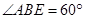 ,所以
,所以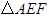 是等边三角形,
是等边三角形,
又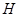 是线段
是线段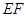 的中点,所以
的中点,所以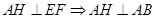 , 1分
, 1分
因为平面
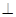 平面
平面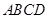 ,所以
,所以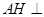 平面
平面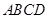 ,所以
,所以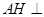
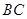 ; 3分
; 3分
在直角梯形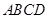 中,
中,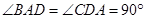 ,得到:
,得到: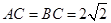 ,从而
,从而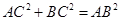 ,所以
,所以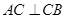 ,所以
,所以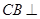 平面
平面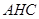 5分,
5分,
又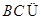 平面
平面 ,所以平面
,所以平面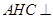 平面
平面 7分
7分
(2)存在,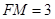
证明:设线段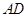 的中点为
的中点为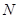 ,
,
则梯形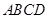 中,得到:
中,得到: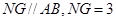 , 9分
, 9分
又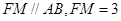 ,所以
,所以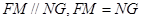 ,
,
所以四边形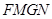 是平行四边形,所以
是平行四边形,所以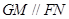 ,
,
又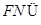 平面
平面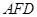 ,
,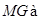 平面
平面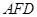 ,所以
,所以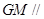 平面
平面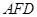 。 12分
。 12分
考点:1.面面垂直的判定定理;2.线面垂直的判定定理;3.线面平行的判定定理.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
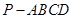 中,底面
中,底面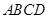 是矩形,
是矩形,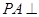 平面
平面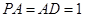 ,
,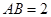 ,
,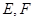 分别是
分别是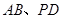 的中点.
的中点.
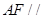 平面
平面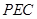 ;
; 的余弦值.
的余弦值.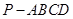 中,侧棱
中,侧棱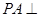 底面
底面 ,底面
,底面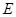 为
为 上一点,
上一点,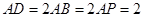 ,
,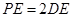 .
.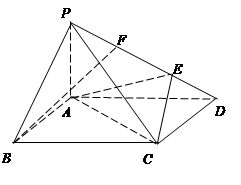
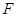 为
为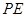 的中点,求证
的中点,求证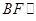 平面
平面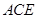 ;
; 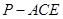 的体积.
的体积. 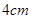 的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,重合后的点记为
的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,重合后的点记为 ,构成一个三棱锥.
,构成一个三棱锥.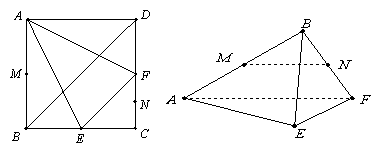
 与平面
与平面 的位置关系,并给出证明;
的位置关系,并给出证明; 平面
平面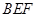 ;
;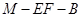 的余弦值.
的余弦值.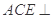 平面
平面 ,四边形
,四边形 .
.
 平面
平面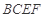 ;
;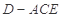 的体积.
的体积. 是矩形
是矩形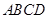 中
中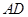 边上的点,
边上的点, 为
为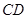 边的中点,
边的中点,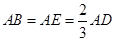 ,现将
,现将 沿
沿 边折至
边折至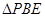 位置,且平面
位置,且平面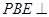 平面
平面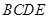 .
. 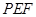 ;
;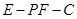 的大小.
的大小. 
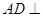 平面
平面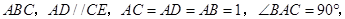 凸多面体
凸多面体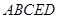 的体积为
的体积为 ,
, 为
为 的中点.
的中点.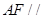 平面
平面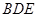 ;
;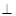 平面
平面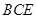 .
. 
 中(图1),
中(图1),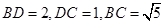 ,
,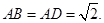
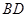 中点为
中点为 ,将图1沿直线
,将图1沿直线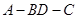 为
为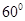 (图2)
(图2)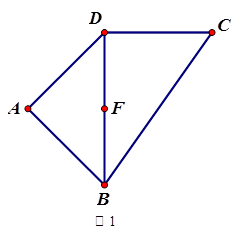
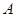 作直线
作直线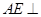 平面
平面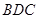 ,且
,且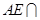 平面
平面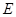 ,求
,求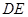 的长度。
的长度。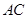 与平面
与平面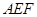 所成角的正弦值。
所成角的正弦值。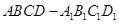 中,
中,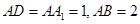 ,点E为AB的中点.
,点E为AB的中点.
 与平面
与平面 所成的角;
所成的角;  的平面角的正切值.
的平面角的正切值.