题目内容
19．一动圆P与圆C1：x2+y2+6x+5=0外切，同时与圆C2：x2+y2-6x-91=0内切，记该动圆圆心P的轨迹为曲线C，若点M为曲线C上的任一点，则|MC2|的最大值为9．分析 求出两个圆的圆心与半径，设出动圆的圆心与半径，判断动圆的圆心轨迹，推出结果即可．
解答 解：圆x2+y2+6x+5=0的圆心为C1（-3，0），半径为2；
圆x2+y2-6x-91=0的圆心为C2（3，0），半径为10；
设动圆圆心为M（x，y），半径为x；
则MC1=2+r，MC2=10-r；
于是MC1+MC2=12＞C1C2=6
所以，动圆圆心M的轨迹是以C1（-3，0），C2（3，0）为焦点，长轴长为12的椭圆．
a=6，c=3，b2=a2-c2=27；
所以M的轨迹方程为$\frac{{x}^{2}}{36}$$+\frac{{y}^{2}}{27}$=1．
|MC2|的最大值为：a+c=9．
故答案为：9．
点评 本题考查轨迹方程的求法，直线与椭圆的位置关系的应用，考查分析问题解决问题的能力，转化思想的应．．
练习册系列答案
阅读快车系列答案
相关题目
7．计算：$\frac{1-co{s}^{2}10°}{cos80°•\sqrt{1-cos20°}}$=（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | $\frac{1}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | -$\frac{\sqrt{2}}{2}$ |
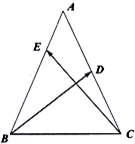如图，在△ABC中，已知AB=AC=$\sqrt{6}$，AD=DC，$\overrightarrow{AB}$=3$\overrightarrow{AE}$，若$\overrightarrow{BD}•\overrightarrow{AC}$=-$\frac{1}{2}$，则$\overrightarrow{BD}•\overrightarrow{CE}$等于$-\frac{11}{12}$．
8．为了得到函数y=3cos（2x+$\frac{π}{3}$），x∈R的图象，只需把函数y=3cos2x的图象（ ）
| A． | 向左平行移动$\frac{π}{3}$个单位长度 | B． | 向右平行移动$\frac{π}{3}$个单位长度 | ||
| C． | 向左平行移动$\frac{π}{6}$个单位长度 | D． | 向右平行移动$\frac{π}{6}$个单位长度 |