题目内容
(本题满分12分)已知椭圆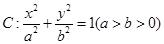 过点
过点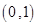 ,且离心率为
,且离心率为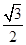 .
.
(Ⅰ)求椭圆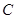 的方程;
的方程;
(Ⅱ)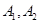 为椭圆
为椭圆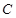 的左、右顶点,直线
的左、右顶点,直线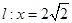 与
与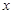 轴交于点
轴交于点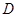 ,点
,点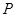 是椭圆
是椭圆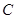 上异于
上异于
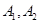 的动点,直线
的动点,直线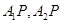 分别交直线
分别交直线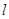 于
于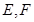 两点.证明:
两点.证明: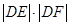 恒为定值.
恒为定值.
【答案】
(Ⅰ)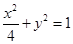 . (Ⅱ)
. (Ⅱ)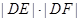 为定值
为定值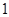 .证明见解析。
.证明见解析。
【解析】本试题主要是考出了椭圆方程的求解,椭圆的几何性质,直线与椭圆的位置关系的运用的综合考查,体现了运用代数的方法解决解析几何的本质的运用。
(1)首先根据题意的几何性质来表示得到关于a,b,c的关系式,从而得到其椭圆的方程。
(2设出直线方程,设点P的坐标,点斜式得到AP的方程,然后联立方程组,可知借助于韦达定理表示出长度,进而证明为定值。
(Ⅰ)解:由题意可知,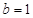 ,
,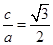 ,
,
解得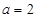 .
…………4分
.
…………4分
所以椭圆的方程为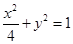 . …………5分
. …………5分
(Ⅱ)证明:由(Ⅰ)可知,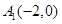 ,
,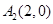 .设
.设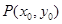 ,依题意
,依题意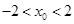 ,
,
于是直线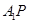 的方程为
的方程为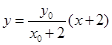 ,令
,令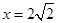 ,则
,则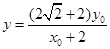 .
.
即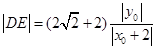 .
…………7分
.
…………7分
又直线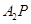 的方程为
的方程为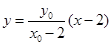 ,令
,令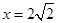 ,则
,则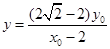 ,
,
即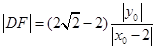 .
…………9分
.
…………9分
 …………11分
…………11分
又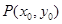 在
在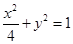 上,所以
上,所以 ,即
,即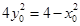 ,代入上式,
,代入上式,
得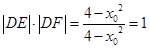 ,所以
,所以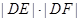 为定值
为定值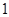 . …………12分
. …………12分

练习册系列答案
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
 的三个内角
的三个内角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 .
. ,且
,且 .(1)求
.(1)求 .求
.求 .
. ,
, 的等比中项。
的等比中项。 是等差数列;(2)若
是等差数列;(2)若 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。 :
: 的长轴长是短轴长的
的长轴长是短轴长的 倍,
倍, ,
, 是它的左,右焦点.
是它的左,右焦点. ,且
,且 ,
, ,求
,求 作以
作以 (
( 是切点),且使
是切点),且使 ,求动点
,求动点 的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量
的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量 与
与 是共线向量
是共线向量 分别是左右焦点,求
分别是左右焦点,求 的取值范围
的取值范围