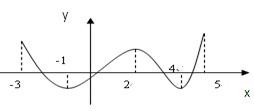
题目内容
函数 的单调递增区间是________.
的单调递增区间是________.
 (开闭区间都可)
(开闭区间都可)分析:利用两角差的正弦公式,把函数的解析式化为 2sin(x-
 ),由2kπ-
),由2kπ- ≤x-
≤x- ≤2kπ+
≤2kπ+ ,k∈z,解得x的范围,即为函数的增区间;再由x∈[-π,0]进一步确定函数的增区间.
,k∈z,解得x的范围,即为函数的增区间;再由x∈[-π,0]进一步确定函数的增区间.解答:函数
 =2sin(x-
=2sin(x- ),
),由2kπ-
 ≤x-
≤x- ≤2kπ+
≤2kπ+ ,k∈z,解得 2kπ-
,k∈z,解得 2kπ- ≤x≤2kπ+
≤x≤2kπ+ ,k∈z.
,k∈z.又x∈[-π,0],
∴单调增区间为
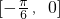 .
.故答案为:
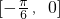 .
.点评:本题主要考查两角差的正弦公式,正弦函数的单调性,把函数的解析式化为 2sin(x-
 )是解题的关键.
)是解题的关键. 
练习册系列答案
相关题目