题目内容
9.已知函数f(x)=x2-8lnx,g(x)=-x2+14x.(Ⅰ)求函数f(x)在点(1,f(1))处的切线方程;
(Ⅱ)若函数f(x)与g(x)在区间(a,a+1)上均为增函数,求a的取值范围;
(Ⅲ)设x≥1,讨论曲线y=f(x)与曲线y=g(x)+m公共点的个数.
分析 (Ⅰ)因为f'(x)=2x-$\frac{8}{x}$,求出切线的斜率.继而得到切线方程.
(Ⅱ)因为f'(x)=$\frac{2(x+2)(x-2)}{x}$,求出函数f(x)的单调区间,又由题意知有含参数的单调区间,继而求出参数范围.
(Ⅲ)当x≥1时,曲线y=f(x)与曲线y=g(x)+m公共点的个数方程2x2-8lnx-14x=m根的个数.转化思路,对曲线y=f(x)与曲线y=g(x)+m公共点的个数讨论.
解答 解:(Ⅰ)因为f'(x)=2x-$\frac{8}{x}$,所以切线的斜率k=f'(1)=-6…(2分)
又f(1)=1,故所求切线方程为y-1=-6(x-1),即y=-6x+7 …(4分)
(Ⅱ)因为f'(x)=$\frac{2(x+2)(x-2)}{x}$,又x>0,所以当x>2时,f'(x)>0;
当0<x<2时,f'(x)<0.即f(x)在(2,+∞)上递增,在(0,2)上递减…(6分)
又g(x)=-(x-7)2+49,所以g(x)在(-∞)上递增,在(7,+∞)上递减…(7分)
欲f(x)与g(x)在区间(a,a+1)上均为增函数,则$\left\{\begin{array}{l}{a≥2}\\{a+1≤7}\end{array}\right.$,
解得2≤x≤6…(8分)
(Ⅲ)当x≥1时,曲线y=f(x)与曲线y=g(x)+m公共点的个数方程2x2-8lnx-14x=m根的个数,
令h(x)=2x2-8lnx-14x,方程即为h(x)=m.
又$h'(x)=4x-\frac{8}{x}-14=\frac{2(x-4)(2x+1)}{x}$,且x>0,所以当x>4时,h'(x)>0;
当0<x<4时,h'(x)<0,即h(x)在(4,+∞)上递增,在(0,4)上递减.
故h(x)在x=4处取得最小值,且h(1)=-12 …(10分)
所以对曲线y=f(x)与曲线y=g(x)+m公共点的个数,讨论如下:
当m∈(-∞,-16ln2-24)时,有0个公共点;
当m=-16ln2-24或m∈(-12,+∞)时,有1个公共点;
当m∈(-16ln2-24,-12]时,有2个公共点.…(12分)
点评 本题主要考查导数的几何意义和利用导数求参数的取值范围等问题,属于难题,在高考中常以压轴题出现.

| A. | 11 | B. | 66 | C. | 76 | D. | 134 |
| A. | -i | B. | -1 | C. | i | D. | 1 |
| A. | [2$\sqrt{2}$,4) | B. | [2$\sqrt{2}$,$\sqrt{2}$+2] | C. | (-∞,2$\sqrt{2}$] | D. | [2$\sqrt{2}$,+∞) |
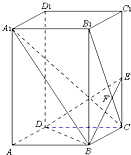 如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.
如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F. 如图,在△ABC中,AC=12,∠ABC=2∠C.
如图,在△ABC中,AC=12,∠ABC=2∠C.