Question

已知正方形ABCD的边长为1，PD⊥平面ABCD，且PD=1，E、F分别为AB、BC的中点.

(1)求点D到平面PEF的距离；

（2）求直线AC到平面PEF的距离.

Answer 1

解：（1）如图，建立空间直角坐标系，则P（0，0，1），A（1，0，0），C（0，1，0），E（1，，0），F（，1，0）.?

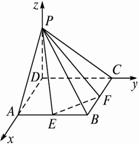
设DH⊥平面PEF,垂足为H，则?

=x+y+z(x+y+z=1)?

=(x+y,+y,z).?

=(1,,-1),=(,1,-1).?

∴·=x+y+(x+y)-z=x+y-z=0.?

同理，x+y-z=0,?

又∵x+y+z=1,?

∴可解得x=y=,z=.?

∴=(2,2,3).?

∴=.?

(2)设AH′⊥平面PEF，垂足为H′.则∥，设=λ(2,2,3)=(2λ,2λ,3λ)（λ≠0）,则=+=(0,-,0)+(2λ,2λ,3λ)?

=(2λ,2λ-,3λ),?

∴?·=4λ²+4λ²-λ+9λ²=0,?

即λ=.?

∴=(2,2,3),||=.?

而AC∥平面PEF，?

因此，点D到平面PEF的距离为；?

AC到平面PEF的距离为.