题目内容
已知椭圆的两焦点为F1(-| 3 |
| 3 |
(1)求此椭圆方程.
(2)若∠F1PF2=
| π |
| 3 |
分析:(1)根据题意可求得a和c,进而根据b,a和c的关系,则b可得,进而求得椭圆的方程.
(2)由余弦定理结合椭圆的定义,经整体运算可求得|PF1|•|PF2|的值,进而求其面积.
(2)由余弦定理结合椭圆的定义,经整体运算可求得|PF1|•|PF2|的值,进而求其面积.
解答:解:(1)依题意得c=
,2a=4,
解得a=2,c=
,从而b=1.
故椭圆的方程为
+
=1.
(2)在△F1PF2中,由余弦定理得|F1F2|2=|PF1|2+|PF2|2-2|PF1|•|PF2|cos60°,
∴|PF1|2+|PF2|2-|PF1|•|PF2|=(2c)2=(2
)2=12 ①
又|PF1|+|PF2|=2a=4,平方得|PF1|2+|PF2|2+2|PF1|•|PF2|=16,=2 ②,
②-①得3|PF1|•|PF2|=4,即 |PF1|•|PF2|=
,
∴△F1PF2的面积 S=
|PF1|•|PF2|sin60°=
.
∴∠F1PF2=
,△F1PF2的面积
.
| 3 |
解得a=2,c=
| 3 |
故椭圆的方程为
| x2 |
| 4 |
| y2 |
| 1 |
(2)在△F1PF2中,由余弦定理得|F1F2|2=|PF1|2+|PF2|2-2|PF1|•|PF2|cos60°,
∴|PF1|2+|PF2|2-|PF1|•|PF2|=(2c)2=(2
| 3 |
又|PF1|+|PF2|=2a=4,平方得|PF1|2+|PF2|2+2|PF1|•|PF2|=16,=2 ②,
②-①得3|PF1|•|PF2|=4,即 |PF1|•|PF2|=
| 4 |
| 3 |
∴△F1PF2的面积 S=
| 1 |
| 2 |
| ||
| 3 |
∴∠F1PF2=
| π |
| 3 |
| ||
| 3 |
点评:本题考查椭圆的简单性质的应用,以及用待定系数法求椭圆的标准方程的方法.还考查直线、圆和椭圆等平面解析几何的基础知识,考查综合运用数学知识进行推理运算的能力和解决问题的能力.本题将圆锥曲线与三角问题巧妙的交汇在一起,事实上,在椭圆中S=b2tanθ,同理可求得在双曲线中 S=
(其中 θ=
).
| b2 |
| tanθ |
| ∠F1PF2 |
| 2 |

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
 的左焦点为F,A(-a,0),B(0,b)为椭圆的两个顶点,若F到AB的距离等于
的左焦点为F,A(-a,0),B(0,b)为椭圆的两个顶点,若F到AB的距离等于 ,则椭圆的离心率为( )
,则椭圆的离心率为( )
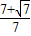


 的右焦点为F(2,0),M为椭圆的上顶点,O为坐标原点,且△MOF是等腰直角三角形.
的右焦点为F(2,0),M为椭圆的上顶点,O为坐标原点,且△MOF是等腰直角三角形. ).
). 的左焦点为F,A(-a,0),B(0,b)为椭圆的两个顶点,若F到AB的距离等于
的左焦点为F,A(-a,0),B(0,b)为椭圆的两个顶点,若F到AB的距离等于 ,则椭圆的离心率为( )
,则椭圆的离心率为( )



 的右焦点为F(2,0),M为椭圆的上顶点,O为坐标原点,且△MOF是等腰直角三角形.
的右焦点为F(2,0),M为椭圆的上顶点,O为坐标原点,且△MOF是等腰直角三角形. ).
). 的左焦点为F,A(-a,0),B(0,b)为椭圆的两个顶点,若F到AB的距离等于
的左焦点为F,A(-a,0),B(0,b)为椭圆的两个顶点,若F到AB的距离等于 ,则椭圆的离心率为( )
,则椭圆的离心率为( )


