题目内容
已知函数f(x)=loga(2x-a)在区间[ ,
, ]上恒有f(x)>0,则实数a的取值范围是
]上恒有f(x)>0,则实数a的取值范围是
- A.[
 ,1]
,1] - B.[
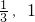 )
) - C.(
 ,1]
,1] - D.(
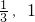 )
)
D
分析:根据对数函数的图象和性质可得,函数f(x)=loga(2x-a)在区间[ ,
, ]上恒有f(x)>0,即
]上恒有f(x)>0,即 ,或
,或 ,分别在不等式组,综合讨论结果,可得答案.
,分别在不等式组,综合讨论结果,可得答案.
解答:若函数f(x)=loga(2x-a)在区间[ ,
, ]上恒有f(x)>0,
]上恒有f(x)>0,
则 ,或
,或
当 时,解得
时,解得 <a<1
<a<1
当 时,不等式无解
时,不等式无解
综上实数a的取值范围是(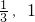 )
)
故选D
点评:本题考查的知识点是复合函数的单调性,及不等式的解法,其中根据对数函数的图象和性质构造不等式组是解答的关键.
分析:根据对数函数的图象和性质可得,函数f(x)=loga(2x-a)在区间[
 ,
, ]上恒有f(x)>0,即
]上恒有f(x)>0,即 ,或
,或 ,分别在不等式组,综合讨论结果,可得答案.
,分别在不等式组,综合讨论结果,可得答案.解答:若函数f(x)=loga(2x-a)在区间[
 ,
, ]上恒有f(x)>0,
]上恒有f(x)>0,则
 ,或
,或
当
 时,解得
时,解得 <a<1
<a<1当
 时,不等式无解
时,不等式无解综上实数a的取值范围是(
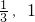 )
)故选D
点评:本题考查的知识点是复合函数的单调性,及不等式的解法,其中根据对数函数的图象和性质构造不等式组是解答的关键.

练习册系列答案
相关题目