题目内容
设M是△ABC内任一点,且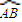
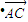 =2
=2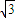 ,∠BAC=30°,设△MBC,△MAC,△MAB的面积分别x,y,z,且Z=
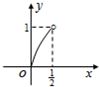
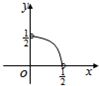
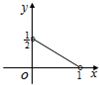
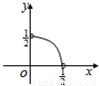
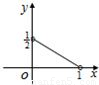
,∠BAC=30°,设△MBC,△MAC,△MAB的面积分别x,y,z,且Z= ,则在平面直角中坐标系中,以x,y为坐标的点(x,y)的轨迹图形是( )
,则在平面直角中坐标系中,以x,y为坐标的点(x,y)的轨迹图形是( )A.
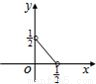
B.
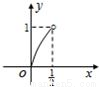
C.
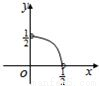
D.
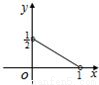
【答案】分析:先求出AB•AC,再求出△ABC的面积,再利用△ABC的面积等于x+y+z及Z= ,可得 x+y=
,可得 x+y= ,
,
0≤x≤ ,0≤y≤
,0≤y≤ .
.
解答:解:∵
 =AB•AC•cos30°=2
=AB•AC•cos30°=2 ,∴AB•AC=4,
,∴AB•AC=4,
△ABC的面积为 AB•AC sin30°=1,由题意知 x+y+z=1,再由Z=
AB•AC sin30°=1,由题意知 x+y+z=1,再由Z= ,
,
∴x+y= ,0≤x≤
,0≤x≤ ,0≤y≤
,0≤y≤ ,
,
故选 A.
点评:本题考查两个向量的数量积的定义,以及三角形的面积公式的应用,直线的一般式方程的特征.
 ,可得 x+y=
,可得 x+y= ,
,0≤x≤
 ,0≤y≤
,0≤y≤ .
.解答:解:∵

 =AB•AC•cos30°=2
=AB•AC•cos30°=2 ,∴AB•AC=4,
,∴AB•AC=4,△ABC的面积为
 AB•AC sin30°=1,由题意知 x+y+z=1,再由Z=
AB•AC sin30°=1,由题意知 x+y+z=1,再由Z= ,
,∴x+y=
 ,0≤x≤
,0≤x≤ ,0≤y≤
,0≤y≤ ,
,故选 A.
点评:本题考查两个向量的数量积的定义,以及三角形的面积公式的应用,直线的一般式方程的特征.

练习册系列答案
相关题目

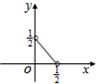
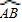
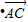 =2
=2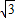 ,∠BAC=30°,设△MBC,△MAC,△MAB的面积分别x,y,z,且Z=
,∠BAC=30°,设△MBC,△MAC,△MAB的面积分别x,y,z,且Z= ,则在平面直角中坐标系中,以x,y为坐标的点(x,y)的轨迹图形是( )
,则在平面直角中坐标系中,以x,y为坐标的点(x,y)的轨迹图形是( )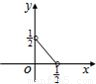
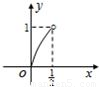

 =2
=2 ,∠BAC=30°,设△MBC,△MAC,△MAB的面积分别x,y,z,且Z=
,∠BAC=30°,设△MBC,△MAC,△MAB的面积分别x,y,z,且Z= ,则在平面直角中坐标系中,以x,y为坐标的点(x,y)的轨迹图形是( )
,则在平面直角中坐标系中,以x,y为坐标的点(x,y)的轨迹图形是( )




 =2
=2 ,∠BAC=30°,设△MBC,△MAC,△MAB的面积分别x,y,z,且Z=
,∠BAC=30°,设△MBC,△MAC,△MAB的面积分别x,y,z,且Z= ,则在平面直角中坐标系中,以x,y为坐标的点(x,y)的轨迹图形是( )
,则在平面直角中坐标系中,以x,y为坐标的点(x,y)的轨迹图形是( )


