题目内容
(本小题满分12分)
已知椭圆C: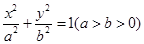 的离心率为
的离心率为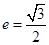 ,A,B分别为椭圆的长轴和短轴的端点,M为AB的中点,O为坐标原点,且
,A,B分别为椭圆的长轴和短轴的端点,M为AB的中点,O为坐标原点,且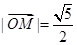 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)过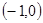 的直线
的直线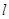 与椭圆交于P、Q两点,求
与椭圆交于P、Q两点,求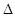 POQ的面积的最大时直线
POQ的面积的最大时直线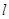 的方程。
的方程。
(1) ;(2)当直线
;(2)当直线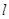 的方程为
的方程为 时,
时,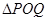 面积最大.
面积最大.
【解析】离心率为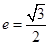 ,列式
,列式 ,
, ,M为AB的中点,O为坐标原点,且
,M为AB的中点,O为坐标原点,且 .三式求解;(Ⅱ)过
.三式求解;(Ⅱ)过 的直线
的直线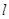 与椭圆交于P、Q两点,求
与椭圆交于P、Q两点,求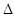 POQ的面积的最大,考查的是弦长公式,点到直线的距离,列出关于
POQ的面积的最大,考查的是弦长公式,点到直线的距离,列出关于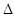 POQ的面积公式,均值定理求解。
POQ的面积公式,均值定理求解。
解:(Ⅰ)设椭圆的半焦距为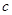 ,则
,则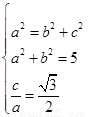 ,解得
,解得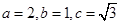 ,所以椭圆的方程为
,所以椭圆的方程为 . ----------4分
. ----------4分
(Ⅱ)方法一:设交点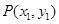 ,
, ,
,
当直线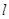 的斜率不存在时,直线
的斜率不存在时,直线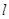 的方程为
的方程为 ,
,
则易得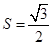 .
--------------6分
.
--------------6分
当直线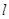 的斜率存在时,设其方程为
的斜率存在时,设其方程为 (
( ),联立椭圆方程
),联立椭圆方程 ,得
,得 ,两个根为
,两个根为
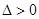 恒成立,
恒成立,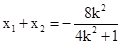 ,
,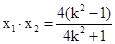 ---------7分
---------7分
则
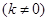 ,
,
又原点到直线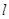 的距离
的距离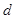 =
=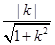 ,
--------------8分
,
--------------8分
所以
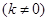
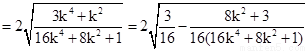
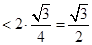 --------------11分
--------------11分
所以,当直线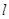 的方程为
的方程为 时,
时,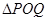 面积最大.
--------------12分
面积最大.
--------------12分
方法二:设交点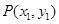 ,
, ,
,
当直线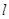 的斜率不存在时,直线
的斜率不存在时,直线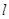 的方程为
的方程为 ,
,
则易得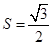 .
----------6分
.
----------6分
当直线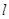 的斜率存在时,设其方程为
的斜率存在时,设其方程为 (
( ),联立椭圆方程
),联立椭圆方程 ,得
,得
 ,两个根为
,两个根为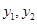 ,
,
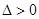 恒成立,
恒成立, ,
-----------7分
,
-----------7分
 ---------------8分
---------------8分
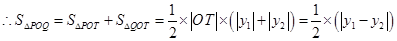
=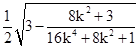
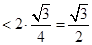 ---------11分
---------11分
所以,当直线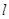 的方程为
的方程为 时,
时,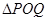 面积最大.
-----------12分
面积最大.
-----------12分

 阅读快车系列答案
阅读快车系列答案