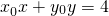题目内容
圆x2+y2=2的经过点P(
,2-
)的切线方程是( )
| 2 |
| 2 |
分析:由圆的方程,找出圆心A坐标和半径r,由P的坐标求出P到圆心的距离|AP|,与圆的半径比较大小得出P在圆外,分两种情况考虑:当过P的切线方程的斜率不存在时,显然切线方程为x=
;若过P的切线方程的斜率存在时,设切线方程的斜率为k,由P的坐标及k,表示出直线的方程,根据圆心到切线的距离等于圆的半径,利用点到直线的距离公式列出关于k的方程,求出方程的解得到k的值,确定出切线的方程,综上,得到所有满足题意的切线方程.
| 2 |
解答:解:由圆x2+y2=2,得到圆心A(0,0),半径r=
,
又P(
,2-
),
∴|AP|=
=2
>
=r,
∴P在圆A外,
若过P的切线方程的斜率不存在时,显然切线方程为x=
,
若过P的切线方程的斜率存在时,设切线方程的斜率为k,
可得切线方程为y-(2-
)=k(x-
),即kx-y+2-
k-
=0,
∴圆心A到切线的距离d=r,即|2-
k-
|=
,
两边平方得:(2-
k-
)2=2(1+k2),
解得:k=-1,
∴切线方程为-x-y+2=0,即x+y=2,
综上,过P的与圆相切的直线方程为x=
或x+y=2.
故选C
| 2 |
又P(
| 2 |
| 2 |
∴|AP|=
(
|
2-
|
| 2 |
∴P在圆A外,
若过P的切线方程的斜率不存在时,显然切线方程为x=
| 2 |
若过P的切线方程的斜率存在时,设切线方程的斜率为k,
可得切线方程为y-(2-
| 2 |
| 2 |
| 2 |
| 2 |
∴圆心A到切线的距离d=r,即|2-
| 2 |
| 2 |
| 2(1+k2) |
两边平方得:(2-
| 2 |
| 2 |
解得:k=-1,
∴切线方程为-x-y+2=0,即x+y=2,
综上,过P的与圆相切的直线方程为x=
| 2 |
故选C
点评:此题考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,两点间的距离公式,点与圆的位置关系,点到直线的距离公式,直线的点斜式方程,利用了分类讨论的数学思想,当直线与圆相切时,圆心到直线的距离等于圆的半径,熟练掌握此性质是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目