题目内容
已知抛物线 :
: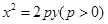 上一点
上一点 到其焦点的距离为
到其焦点的距离为 .
.
(I)求 与
与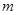 的值;
的值;
(II)设抛物线 上一点
上一点 的横坐标为
的横坐标为 ,过
,过 的直线交
的直线交 于另一点
于另一点 ,交
,交 轴于点
轴于点 ,过点
,过点 作
作 的垂线交
的垂线交 于另一点
于另一点 .若
.若 是
是 的切线,求
的切线,求 的最小值.
的最小值.
【答案】
(1)  ,
,
(2) 
【解析】解(Ⅰ)由抛物线方程得其准线方程: ,根据抛物线定义
,根据抛物线定义
点 到焦点的距离等于它到准线的距离,即
到焦点的距离等于它到准线的距离,即 ,解得
,解得 ……3分
……3分
 抛物线方程为:
抛物线方程为: ,将
,将 代入抛物线方程,解得
代入抛物线方程,解得 ………………5分
………………5分
(Ⅱ)由题意知,过点 的直线
的直线 斜率存在且不为0,设其为
斜率存在且不为0,设其为 。
。
则 ,当
,当 则
则 。
。
联立方程 ,整理得:
,整理得: ……………7分
……………7分
即: ,解得
,解得 或
或
 ,而
,而 ,
, 直线
直线 斜率为
斜率为
 ,
,
联立方程 …………9分
…………9分
整理得: ,即:
,即:
 ,解得:
,解得: ,或
,或
 ,
,
而抛物线在点N处切线斜率:
 MN是抛物线的切线,
MN是抛物线的切线, ,
,
 整理得
整理得 …………………………………12分
…………………………………12分
 ,解得
,解得 (舍去),或
(舍去),或 ,
, ……14分
……14分

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 :
: 上一点
上一点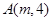 到其焦点的距离为
到其焦点的距离为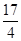 .
. 与
与 的值;
的值; 的横坐标为
的横坐标为 ,过
,过 ,交
,交 轴于点
轴于点 ,过点
,过点 的垂线交
的垂线交 .若
.若 是
是 的最小值.
的最小值.