题目内容
(2012•广东模拟)
dx=
.
| ∫ | 0 -1 |
| 1-x2 |
| π |
| 4 |
| π |
| 4 |
分析:
dx的几何意义是圆x2+y2=1在第二象限的部分与坐标轴围成的图形的面积,由此可得结论.
| ∫ | 0 -1 |
| 1-x2 |
解答:解:
dx的几何意义是圆x2+y2=1在第二象限的部分与坐标轴围成的图形的面积
∴:
dx=
×π=
故答案为:
| ∫ | 0 -1 |
| 1-x2 |
∴:
| ∫ | 0 -1 |
| 1-x2 |
| 1 |
| 4 |
| π |
| 4 |
故答案为:
| π |
| 4 |
点评:本题考查利用定积分求面积,解题的关键是明确定积分的几何意义,属于基础题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
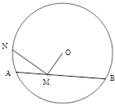 (2012•广东模拟)(几何证明选讲选做题)如图,点M为⊙O的弦AB上的一点,连接MO.MN⊥OM,MN交圆于N,若MA=2,MB=4,则MN=
(2012•广东模拟)(几何证明选讲选做题)如图,点M为⊙O的弦AB上的一点,连接MO.MN⊥OM,MN交圆于N,若MA=2,MB=4,则MN=