题目内容
已知函数f（x）=3x+k（k为常数），A（－2k，2）是函数y= f －1（x）图象上的点.
（1）求实数k的值及函数f －1（x）的解析式；
（2）将y= f －1（x）的图象按向量a=（3，0）平移，得到函数y=g（x）的图象，若2 f －1（x+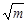
－3）－g（x）≥1恒成立，试求实数m的取值范围.
【答案】
（1）f －1（x）=log3（x+3）（x＞－3）.（2）m≥
.
【解析】主要考查指数函数、对数函数互为反函数关系、反函数概念及反函数求法。
解：（1）∵A（－2k，2）是函数y= f －1（x）图象上的点，
∴B（2，－2k）是函数y=f（x）上的点.
∴－2k=32+k.∴k=－3.
∴f（x）=3x－3.
∴y= f －1（x）=log3（x+3）（x＞－3）.
（2）将y= f －1（x）的图象按向量a=（3，0）平移，得到函数y=g（x）=log3x（x＞0），要使2 f －1（x+
－3）－g（x）≥1恒成立，即使2log3（x+）－log3x≥1恒成立，所以有x+
+2≥3在x＞0时恒成立，只要（x++2）min≥3.
又x+≥2（当且仅当x=，即x=时等号成立），∴（x++2）min=4，即4≥3.∴m≥.
练习册系列答案
相关题目
已知函数f（x）=3•2x-1，则当x∈N时，数列{f（n+1）-f（n）}（ ）
| A、是等比数列 | B、是等差数列 | C、从第2项起是等比数列 | D、是常数列 |