题目内容
已知正三棱锥S-ABC的侧棱与底面边长相等,E,F分别为SC,AB的中点,则异面直线EF与SA所成角的大小是
.
| π |
| 4 |
| π |
| 4 |
分析:线根据题意正确的做出图形在取AC得中点G连接AE,EF,FG,GE,BG则根据异面直线所成的角的定义可得∠FEG或其补角即为异面直线EF与SA所成角,最后再通过解三角形求出∠FEG即可.
解答:解:设正三棱锥S-ABC的侧棱长为a则SA=SB=SC=AB=BC=AC=a
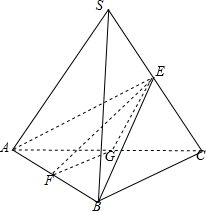
(如上图)取AC得中点G连接AE,EF,FG,GE,BG
∵E,F分别为SC,AB的中点
∴FG
BC,GE
SA且FG=
a=GE
∴∠FEG或其补角即为异面直线EF与SA所成角
∵正三棱锥S-ABC的侧棱与底面边长相等,E,F分别为SC,AB的中点
∴EA=EB
∴EF⊥AB
∵EA=
=
a,AF=
a
∴EF=
=
a
∴FG2+GE2=EF2
∵FG=GE
∴∠FEG=
故答案为

(如上图)取AC得中点G连接AE,EF,FG,GE,BG
∵E,F分别为SC,AB的中点
∴FG
| ∥ |
. |
| ∥ |
. |
| 1 |
| 2 |
∴∠FEG或其补角即为异面直线EF与SA所成角
∵正三棱锥S-ABC的侧棱与底面边长相等,E,F分别为SC,AB的中点
∴EA=EB
∴EF⊥AB
∵EA=
| SA2-SE2 |
| ||
| 2 |
| 1 |
| 2 |
∴EF=
| EA2-AF2 |
| ||
| 2 |
∴FG2+GE2=EF2
∵FG=GE
∴∠FEG=
| π |
| 4 |
故答案为
| π |
| 4 |
点评:本题主要考察了求异面直线所成的角,属常考题型,较难.解题的关键是根据异面直线所成的角的定义做出异面直线EF与SA所成角的平面角但要注意的是异面直线所成的角的范围(0,
]!
| π |
| 2 |

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目







