题目内容
 (2011•顺义区二模)已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=AC=
(2011•顺义区二模)已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=AC=| 1 | 2 |
上一点,AB=4AN,M,D,S分别为PB,AB,BC的中点.
(1)求证:PA∥平面CDM;
(2)求证:SN⊥平面CDM;
(3)求二面角D-MC-N的大小.
分析:(1)在三棱锥P-ABC中,由M,D,分别为PB,AB的中点,知MD∥PA,由此能够证明PA∥平面CMD.
(2)因为M,D,分别为PB,AB的中点,所以MD∥PA.因为PA⊥平面ABC所以MD⊥平面ABC,又SN?平面ABC,所以MD⊥SN.设PA=1,以A为原点,AB,AC,AP所在直线分别为x,y,z轴建立空间直角坐标系.则P(0,0,1),C(0,1,0),B(2,0,0),M(1,0,
),N(
,0,0),S(1,
,0),由向量法能够证明SN⊥平面CMD.
(3)
=(-
,-
,0)是面CMD的一个法向量,设面MCN的法向量
=(x,y,z),由
•
=0,
•
=0,得到
=(-1,-
,1),由此能求出二面角D-MC-N的大小.
(2)因为M,D,分别为PB,AB的中点,所以MD∥PA.因为PA⊥平面ABC所以MD⊥平面ABC,又SN?平面ABC,所以MD⊥SN.设PA=1,以A为原点,AB,AC,AP所在直线分别为x,y,z轴建立空间直角坐标系.则P(0,0,1),C(0,1,0),B(2,0,0),M(1,0,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)
| SN |
| 1 |
| 2 |
| 1 |
| 2 |
| n |
| n |
| CM |
| n |
| CN |
| n |
| 1 |
| 2 |
解答: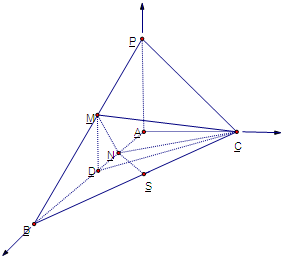 (1)证明:在三棱锥P-ABC中,
(1)证明:在三棱锥P-ABC中,
因为M,D,分别为PB,AB的中点,所以MD∥PA,
因为MD?平面CMD,PA?平面CMD,
所以PA∥平面CMD.
(2)证明:因为M,D,分别为PB,AB的中点,
所以MD∥PA,
因为PA⊥平面ABC所以MD⊥平面ABC,
又SN?平面ABC所以MD⊥SN.…(6分)
设PA=1,以A为原点,AB,AC,AP所在直线分别为x,y,z轴,
建立空间直角坐标系.如图所示,
则P(0,0,1),C(0,1,0),B(2,0,0),
M(1,0,
),N(
,0,0),S(1,
,0),
所以
=(1,-1,
),
=(-
,-
,0),
因为
•
=-
+
+0=0,
所以CM⊥SN.…(9分)
又CM∩MD=M,
所以SN⊥平面CMD.…(10分)
(3)解:由(2)知,
=(-
,-
,0)是平面CMD的一个法向量,
设平面MCN的法向量
=(x,y,z),则
•
=0,
•
=0,
即
,
所以
,令z=1,则x=-1,y=-
,
所以
=(-1,-
,1),
从而cos?
,
>=
=
,
因为二面角D-MC-N为锐角.
所以二面角D-MC-N的大小为
.…..(14分)
 (1)证明:在三棱锥P-ABC中,
(1)证明:在三棱锥P-ABC中,因为M,D,分别为PB,AB的中点,所以MD∥PA,
因为MD?平面CMD,PA?平面CMD,
所以PA∥平面CMD.
(2)证明:因为M,D,分别为PB,AB的中点,
所以MD∥PA,
因为PA⊥平面ABC所以MD⊥平面ABC,
又SN?平面ABC所以MD⊥SN.…(6分)
设PA=1,以A为原点,AB,AC,AP所在直线分别为x,y,z轴,
建立空间直角坐标系.如图所示,
则P(0,0,1),C(0,1,0),B(2,0,0),
M(1,0,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以
| CM |
| 1 |
| 2 |
| SN |
| 1 |
| 2 |
| 1 |
| 2 |
因为
| CM |
| SN |
| 1 |
| 2 |
| 1 |
| 2 |
所以CM⊥SN.…(9分)
又CM∩MD=M,
所以SN⊥平面CMD.…(10分)
(3)解:由(2)知,
| SN |
| 1 |
| 2 |
| 1 |
| 2 |
设平面MCN的法向量
| n |
| n |
| CM |
| n |
| CN |
即
|
所以
|
| 1 |
| 2 |
所以
| n |
| 1 |
| 2 |
从而cos?
| n |
| SN |
| ||||
|
|
| ||
| 2 |
因为二面角D-MC-N为锐角.
所以二面角D-MC-N的大小为
| π |
| 4 |
点评:本题考查PA∥平面CDM的证明,求证SN⊥平面CDM,求二面角D-MC-N的大小.考查运算求解能力,推理论证能力;考查化归与转化思想.解题时要认真审题,仔细解答,注意向量法的合理运用.

练习册系列答案
相关题目
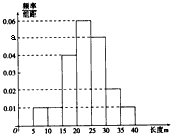 (2011•顺义区二模)某棉纺厂为了解一批棉花的质量,从中随机抽测100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标).所得数据均在区间[5,40]中,其频率分布直方图如图所示,由图中数据可知a=
(2011•顺义区二模)某棉纺厂为了解一批棉花的质量,从中随机抽测100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标).所得数据均在区间[5,40]中,其频率分布直方图如图所示,由图中数据可知a=