Question

如图，AB为圆O的直径，点E、F在圆O上，且AB∥EF，矩形ABCD所在的平面与圆O所在的平面互相垂直，已知AB=2，AD=EF=1．
（Ⅰ）设FC的中点为M，求证：OM∥平面DAF；
（Ⅱ）设平面CBF将几何体EF-ABCD分割成的两个锥体的体积分别为V_F-ABCD、V_F-CBE，求V_F-ABCD：V_F-CBE的值．

Answer 1

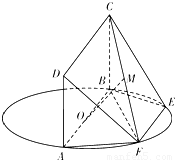
【答案】分析：（Ⅰ）如图，设FD的中点为N，连结AN，MN，证明MNAO为平行四边形，可得OM∥AN．再利用直线和平面平行的判定定理证得 OM∥平面DAF．
（Ⅱ）如图，过点F作FG⊥AB于G，可得FG⊥平面ABCD．先求得 V_F-ABCD 的值，再用等体积法求得V_F-CBE=V_C-BEF= S_△BEF•CB的值，可得 V_F-ABCD：V_F-CBE 的值．
解答：解：（Ⅰ）如图，设FD的中点为N，连结AN，MN．
∵M为FC的中点，∴MN∥CD，MN=CD．
又AO∥CD，AO=CD，∴MN∥AO，MN=AO，
∴MNAO为平行四边形，∴OM∥AN．
又OM?平面DAF，AN?平面DAF，∴OM∥平面DAF．…（6分）
（Ⅱ）如图，过点F作FG⊥AB于G，∵平面ABCD⊥平面ABEF，∴FG⊥平面ABCD．
∴V_F-ABCD= S_ABCD•FG=FG．
∵CB⊥平面ABEF，∴V_F-CBE=V_C-BEF= S_△BEF•CB=•EF•FG•CB=FG．
∴V_F-ABCD：V_F-CBE=：=4．…（13分）
点评：本题主要考查直线和平面平行的判定定理的应用，用等体积法求棱椎的体积，属于中档题．