题目内容
【题目】已知单调递增的等比数列{an}满足a2+a3+a4=28,且a3+2是a2,a4的等差中项.
(1)求数列{an}的通项公式;
(2)若bn=![]() ,Sn=b1+b2+…+bn,对任意正整数n,Sn+(n+m)an+1<0恒成立,试求m的取值范围.
,Sn=b1+b2+…+bn,对任意正整数n,Sn+(n+m)an+1<0恒成立,试求m的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)将已知条件转化为等比数列的基本量![]() 来表示,通过解方程组得到其值,从而确定通项公式;(2)将数列{an}的通项公式代入可求得
来表示,通过解方程组得到其值,从而确定通项公式;(2)将数列{an}的通项公式代入可求得![]() ,根据特点采用错位相减法求得前n项和
,根据特点采用错位相减法求得前n项和![]() ,代入不等式Sn+(n+m)an+1<0,通过分离参数的方法求得m的取值范围
,代入不等式Sn+(n+m)an+1<0,通过分离参数的方法求得m的取值范围
试题解析:(1)设等比数列![]() 的首项为
的首项为![]() ,公比为
,公比为![]() ,依题意,有
,依题意,有![]() ,代入
,代入
![]() 可得
可得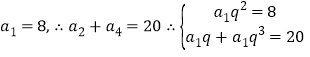 ,解得
,解得![]() 或
或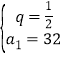 ,又数列
,又数列![]() 单调递增
单调递增![]() ,数列
,数列![]() 的通项公式为
的通项公式为![]()
(2)∵bn=2n·![]() =-n·2n,
=-n·2n,
∴-Sn=1×2+2×22+3×23+…+n×2n,①
-2Sn=1×22+2×23+3×24+…+(n-1)×2n+n×2n+1.②
①-②,得Sn=2+22+23+…+2n-n·2n+1=![]() -n·2n+1=2n+1-n·2n+1-2.
-n·2n+1=2n+1-n·2n+1-2.
∵Sn+(n+m)an+1<0,∴2n+1-n·2n+1-2+n·2n+1+m·2n+1<0对任意正整数n恒成立.
∴m·2n+1<2-2n+1对任意正整数n恒成立,即m<![]() -1恒成立.
-1恒成立.
∵![]() -1>-1,∴m≤-1,即m的取值范围是(-∞,-1].
-1>-1,∴m≤-1,即m的取值范围是(-∞,-1].

练习册系列答案
相关题目