题目内容
已知函数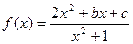
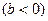 的值域为
的值域为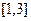 ;
;
(1)、求实数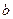 、
、 的值;
的值;
(2)、判断函数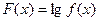 在
在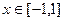 上的单调性,并给出证明;
上的单调性,并给出证明;
(3)、若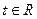 ,求证:
,求证: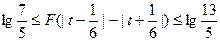 。
。
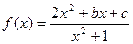
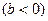 的值域为
的值域为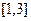 ;
;(1)、求实数
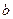 、
、 的值;
的值;(2)、判断函数
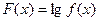 在
在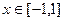 上的单调性,并给出证明;
上的单调性,并给出证明;(3)、若
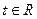 ,求证:
,求证: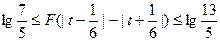 。
。(1) ,
,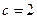 ;(2)减函数(3)见解析
;(2)减函数(3)见解析
 ,
,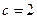 ;(2)减函数(3)见解析
;(2)减函数(3)见解析(1)、由于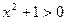 恒成立,∴
恒成立,∴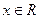 ,
,
令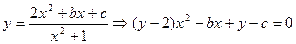 ,
,
则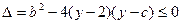 的解集是
的解集是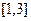 ,
,
故1和3是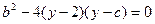 的二根,应用韦达定理求得
的二根,应用韦达定理求得 ,
,
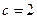 ;
;
(2)、由(1)知,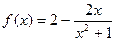 ,应用函数单调性的定义去判断函数
,应用函数单调性的定义去判断函数
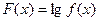 在
在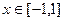 上单调减;
上单调减;
(3)应该注意到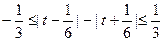 ,则应用(2)的结论,
,则应用(2)的结论,
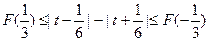 ,即:
,即: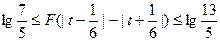 。
。
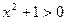 恒成立,∴
恒成立,∴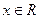 ,
,令
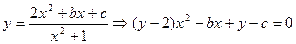 ,
,则
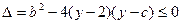 的解集是
的解集是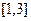 ,
,故1和3是
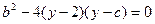 的二根,应用韦达定理求得
的二根,应用韦达定理求得 ,
,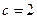 ;
;(2)、由(1)知,
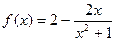 ,应用函数单调性的定义去判断函数
,应用函数单调性的定义去判断函数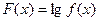 在
在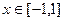 上单调减;
上单调减;(3)应该注意到
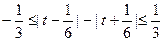 ,则应用(2)的结论,
,则应用(2)的结论,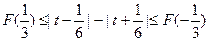 ,即:
,即: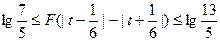 。
。
练习册系列答案
相关题目
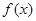 是定义在R上的且以2为周期的偶函数,当
是定义在R上的且以2为周期的偶函数,当 时,
时, ,如果直线
,如果直线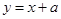 与曲线
与曲线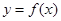 恰有两个不同的交点,则实数
恰有两个不同的交点,则实数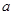 的值为 ( )
的值为 ( )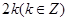
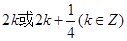
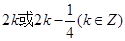
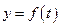 ;
;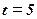 时,第二次服药,问
时,第二次服药,问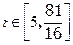 时药效能否持续?
时药效能否持续?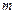 元,变动部分与运行速度V(千米/小时)的平方成正比。比例系数为k(k≠0)。如果机车匀速从甲站开往乙站,为使成本最省应以怎样的速度运行?
元,变动部分与运行速度V(千米/小时)的平方成正比。比例系数为k(k≠0)。如果机车匀速从甲站开往乙站,为使成本最省应以怎样的速度运行?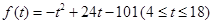 ,
,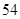 B.
B.
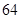 D.
D.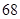
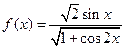 ,
, 的定义域、值域、最小正周期;
的定义域、值域、最小正周期;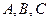 是直线
是直线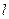 上的三点,点
上的三点,点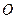 在直线
在直线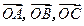 满足
满足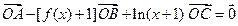 .
.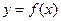 的表达式;
的表达式;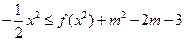 对
对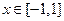 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围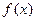 是(-
是(-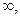 +
+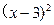 +4,求
+4,求
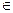 [1,2]时解析式
[1,2]时解析式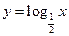 与函数
与函数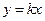 的图象有公共点
的图象有公共点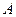 ,且点
,且点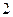 ,
,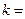 __________.
__________.