题目内容
设函数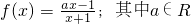 .
.
(Ⅰ)解不等式f(x)≤1;
(Ⅱ)求a的取值范围,使f(x)在区间(0,+∞)上是单调减函数.
解:(Ⅰ)由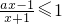 ,化为
,化为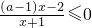 .(1分)
.(1分)
当a=1时,不等式化为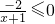 ,解集为{x|x>-1}.(3分)
,解集为{x|x>-1}.(3分)
当a>1时,有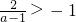 ,解集为
,解集为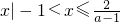 .(5分)
.(5分)
当a=-1时,不等式化为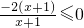 ,解集为{x|x∈R,x≠-1}.(8分)
,解集为{x|x∈R,x≠-1}.(8分)
当a<-1时,有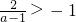 ,a-1<0,
,a-1<0,
不等式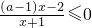 的解集为{x|x<-1,或 x>
的解集为{x|x<-1,或 x>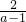 }.(10分)
}.(10分)
(Ⅱ)任取 0<x1<x2,且 则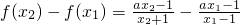 (11分)
(11分)
= .(12分)
.(12分)
因x2>x1故x2-x1>0,又在(0,+∞)上有 x2+1>0,x1+1>0,
∴只有当a+1<0时,即a<-1时.才总有f(x2)-f(x1)<0.
∴当a<-1时,f(x)在(0,+∞)上是单调减函数.(14分)
分析:(Ⅰ)把不等式化为化为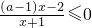 ,分a=1、a>1、a=-1、a<-1四种情况,分别求出解集.
,分a=1、a>1、a=-1、a<-1四种情况,分别求出解集.
(Ⅱ)任意取0<x1<x2,则f(x2)-f(x1)= ,要使f(x)在区间(0,+∞)上是单调减函数,
,要使f(x)在区间(0,+∞)上是单调减函数,
只有a+1<0,由此求得a的取值范围.
点评:本题主要考查分式不等式的解法,函数的单调性的证明方法,体现了分类讨论的数学思想,属于中档题.
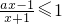 ,化为
,化为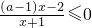 .(1分)
.(1分)当a=1时,不等式化为
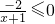 ,解集为{x|x>-1}.(3分)
,解集为{x|x>-1}.(3分)当a>1时,有
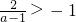 ,解集为
,解集为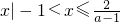 .(5分)
.(5分)当a=-1时,不等式化为
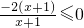 ,解集为{x|x∈R,x≠-1}.(8分)
,解集为{x|x∈R,x≠-1}.(8分)当a<-1时,有
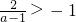 ,a-1<0,
,a-1<0,不等式
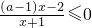 的解集为{x|x<-1,或 x>
的解集为{x|x<-1,或 x>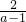 }.(10分)
}.(10分)(Ⅱ)任取 0<x1<x2,且 则
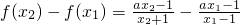 (11分)
(11分)=
 .(12分)
.(12分)因x2>x1故x2-x1>0,又在(0,+∞)上有 x2+1>0,x1+1>0,
∴只有当a+1<0时,即a<-1时.才总有f(x2)-f(x1)<0.
∴当a<-1时,f(x)在(0,+∞)上是单调减函数.(14分)
分析:(Ⅰ)把不等式化为化为
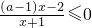 ,分a=1、a>1、a=-1、a<-1四种情况,分别求出解集.
,分a=1、a>1、a=-1、a<-1四种情况,分别求出解集.(Ⅱ)任意取0<x1<x2,则f(x2)-f(x1)=
 ,要使f(x)在区间(0,+∞)上是单调减函数,
,要使f(x)在区间(0,+∞)上是单调减函数,只有a+1<0,由此求得a的取值范围.
点评:本题主要考查分式不等式的解法,函数的单调性的证明方法,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
 (1)当
(1)当 时,求不等式
时,求不等式 的解集;(2)如果不等式
的解集;(2)如果不等式 的解集为
的解集为 ,求
,求 的值。
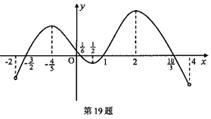
的值。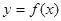 在定义域(—2,4)内可导,其图象
在定义域(—2,4)内可导,其图象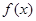 的导函数为
的导函数为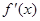 ,则不等
,则不等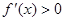 的解集为 。
的解集为 。