题目内容
若loga2<logb2<0,则
- A.0<a<b<1
- B.0<b<a<1
- C.a>b>1
- D.b>a>1
B
分析:利用对数的换底公式,将题中条件:“loga2<logb2<0,”转化成同底数对数进行比较即可.
解答:∵loga2<logb2<0,
由对数换底公式得:
∴
∴0>log2a>log2b
∴根据对数的性质得:
∴0<b<a<1.
故选B.
点评:本题主要考查对数函数的性质,对数函数是许多知识的交汇点,是历年高考的必考内容,在高考中主要考查:定义域、值域、图象、对数方程、对数不等式、对数函数的主要性质(单调性等)及这些知识的综合运用.
分析:利用对数的换底公式,将题中条件:“loga2<logb2<0,”转化成同底数对数进行比较即可.
解答:∵loga2<logb2<0,
由对数换底公式得:
∴

∴0>log2a>log2b
∴根据对数的性质得:
∴0<b<a<1.
故选B.
点评:本题主要考查对数函数的性质,对数函数是许多知识的交汇点,是历年高考的必考内容,在高考中主要考查:定义域、值域、图象、对数方程、对数不等式、对数函数的主要性质(单调性等)及这些知识的综合运用.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目

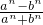 =1(其中n∈N+);
=1(其中n∈N+);
 =1(其中n∈N+);
=1(其中n∈N+);