题目内容
设f(x)= ,则f[f(1)]=________.
,则f[f(1)]=________.
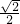
分析:先根据1所在范围得到f(1),再结合f(1)的范围代入对应的解析式即可求出结论.
解答:因为:f(1)=
 ×1-1=-
×1-1=- ;
;∴f[f(1)]=f(-
 )=
)= =
= .
.故答案为:
 .
.点评:本题主要考查分段函数函数值的求法.解决这类问题的关键在于先判断出变量所在范围,进而代入对应的解析式即可.

练习册系列答案
相关题目
题目内容
 ,则f[f(1)]=________.
,则f[f(1)]=________.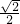
 ×1-1=-
×1-1=- ;
; )=
)= =
= .
. .
.