题目内容
已知有限集
 .如果
.如果 中元素
中元素 满足
满足 ,就称
,就称 为“复活集”,给出下列结论:
为“复活集”,给出下列结论:
①集合 是“复活集”;
是“复活集”;
②若 ,且
,且 是“复活集”,则
是“复活集”,则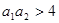 ;
;
③若 ,则
,则 不可能是“复活集”;
不可能是“复活集”;
④若 ,则“复合集”
,则“复合集” 有且只有一个,且
有且只有一个,且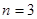 .
.
其中正确的结论是 .(填上你认为所有正确的结论序号).
①③④
解析试题分析: 故①正确;不妨设
故①正确;不妨设 则由韦达定理知
则由韦达定理知 是一元二次方程
是一元二次方程 的两个根,由△>0,可得t<0,或t>4,故②错;不妨设A中
的两个根,由△>0,可得t<0,或t>4,故②错;不妨设A中 由
由
 得
得 当
当 时有
时有 所以
所以 于是
于是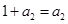 无解即不存在满足条件的复活集故③正确;当n=3时,
无解即不存在满足条件的复活集故③正确;当n=3时, 故只能
故只能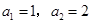 求得
求得 于是复活集A只能有一个
于是复活集A只能有一个 ,当
,当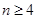 时,由
时,由 即有
即有 也就是说复活集存在的必要条件是:
也就是说复活集存在的必要条件是: 事实上
事实上 矛盾,故④正确.
矛盾,故④正确.
考点:元素与集合,复活集的定义.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
设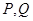 为两个非空集合,定义集合
为两个非空集合,定义集合 ,若
,若 ,
, ,则
,则 中的元素个数是
中的元素个数是
| A.9 | B.7 | C.6 | D.8 |
下列式子中,正确的是( )
A. | B. |
| C.空集是任何集合的真子集 | D. |
设集合 则A∩B= ( )
则A∩B= ( )
| A.ø | B.(3.4) | C.(-2.1) | D.(4.+∞) |
 ,
,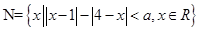
 ,则实的数
,则实的数 取值范围是____________ .
取值范围是____________ .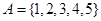
 ,则
,则 中所含元素的个数为 .
中所含元素的个数为 . ,则∁UA=________.
,则∁UA=________. +
+ +
+ 可能取的值组成的集合是________.
可能取的值组成的集合是________.