Question

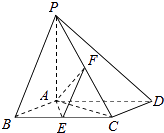
【题目】在四棱锥P﹣ABCD中，底面ABCD是正方形，侧棱PD⊥平面ABCD，AB=PD=a，E为侧棱PC的中点，又作DF⊥PB交PB于点F，则PB与平面EFD所成角为（ ）
A.90°
B.60°
C.45°
D.30°

Answer 1

【答案】A
【解析】解：以D为原点，DA为x轴，DC为y轴，DP为z轴，建立空间直角坐标系D﹣xyz，D为坐标原点．P（0，0，a），B（a，a，0），
=（a，a，﹣a），又 =（0， ， ），
=0+ =0，
∴PB⊥DE．
由已知DF⊥PB，又DF∩DE=D，
∴PB⊥平面EFD，
∴PB与平面EFD所成角为90°．
故选：A．

【考点精析】解答此题的关键在于理解空间角的异面直线所成的角的相关知识，掌握已知为两异面直线，A，C与B，D分别是上的任意两点，所成的角为，则．