题目内容
正方体ABCD-A1B1C1D1中,P为面A1B1C1D1的中心,求证:PA⊥PB1.
如图建立空间直角坐标系D-xyz.?
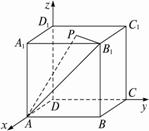
设棱长为1,则A(1,0,0),B1(1,1,1),
,由两点间的距离公式,得
,
,
.
∵|AP|2+|PB1|2=|AB1|2=2,∴AP⊥PB1.
解析:
同答案
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
解析:
口算小状元口算速算天天练系列答案题目内容
正方体ABCD-A1B1C1D1中,P为面A1B1C1D1的中心,求证:PA⊥PB1.
如图建立空间直角坐标系D-xyz.?
设棱长为1,则A(1,0,0),B1(1,1,1),,由两点间的距离公式,得
,,.
∵|AP|2+|PB1|2=|AB1|2=2,∴AP⊥PB1.
同答案
口算小状元口算速算天天练系列答案
如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的：
已知边长为6的正方体ABCD-A1B1C1D1，E，F为AD、CD上靠近D的三等分点，H为BB1上靠近B的三等分点，G是EF的中点．
如图所示，在棱长为2cm的正方体ABCD-A1B1C1D1中，A1B1的中点是P，过点A1作出与截面PBC1平行的截面，简单证明截面形状，并求该截面的面积．
如图，正方体ABCD-A1B1C1D1中，M是棱AB的中点，过A1，M，C三点的平面与CD所成角正弦值（ ）