题目内容
设F1,F2是椭圆 的两个焦点,P是椭圆上一点,若△PF1F2是直角三角形,且|PF1|>|PF2|,则
的两个焦点,P是椭圆上一点,若△PF1F2是直角三角形,且|PF1|>|PF2|,则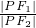 的值为
的值为
- A.2
- B.

- C.

- D.2或

D
分析:当PF2⊥x轴时,求出P的纵坐标,即得|PF2|的值,由椭圆的定义求得|PF1|,进而求得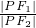 的值.当PF1⊥PF2 时,设|PF2|=m,由椭圆的定义求得|PF1|,由勾股定理可解得m,进而求得
的值.当PF1⊥PF2 时,设|PF2|=m,由椭圆的定义求得|PF1|,由勾股定理可解得m,进而求得 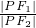 的值.
的值.
解答:由题意得 a=3,b=2,c= ,F1(-
,F1(- ,0),F2 (
,0),F2 (  ,0).
,0).
当PF2⊥x轴时,P的横坐标为 ,其纵坐标为±
,其纵坐标为± ,∴
,∴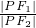 =
= =
= =
= .
.
当PF1⊥PF2 时,设|PF2|=m,则|PF1|=2a-m=6-m,3>m>0,由勾股定理可得
4c2=m2+(6-m)2,即 20=2 m2-12 m+36,解得 m=2 或 m=4(舍去),
故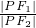 =
= =2.
=2.
综上,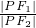 的值等于
的值等于  或2.
或2.
故选D.
点评:本题考查椭圆的定义和标准方程,以及椭圆的简单性质的应用,体现了分类讨论的数学思想,注意考虑PF2⊥x轴时的情况.
分析:当PF2⊥x轴时,求出P的纵坐标,即得|PF2|的值,由椭圆的定义求得|PF1|,进而求得
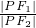 的值.当PF1⊥PF2 时,设|PF2|=m,由椭圆的定义求得|PF1|,由勾股定理可解得m,进而求得
的值.当PF1⊥PF2 时,设|PF2|=m,由椭圆的定义求得|PF1|,由勾股定理可解得m,进而求得 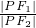 的值.
的值.解答:由题意得 a=3,b=2,c=
 ,F1(-
,F1(- ,0),F2 (
,0),F2 (  ,0).
,0).当PF2⊥x轴时,P的横坐标为
 ,其纵坐标为±
,其纵坐标为± ,∴
,∴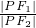 =
= =
= =
= .
.当PF1⊥PF2 时,设|PF2|=m,则|PF1|=2a-m=6-m,3>m>0,由勾股定理可得
4c2=m2+(6-m)2,即 20=2 m2-12 m+36,解得 m=2 或 m=4(舍去),
故
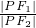 =
= =2.
=2.综上,
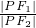 的值等于
的值等于  或2.
或2.故选D.
点评:本题考查椭圆的定义和标准方程,以及椭圆的简单性质的应用,体现了分类讨论的数学思想,注意考虑PF2⊥x轴时的情况.

练习册系列答案
相关题目
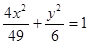 的两个焦点,P是椭圆上的点,且
的两个焦点,P是椭圆上的点,且 ,
, 的面积为( )
的面积为( ) D.
D.