题目内容
已知函数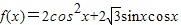 .求
.求(1)函数f(x)的最小正周期;
(2)函数f(x)的单调递减区间;
(3)函数f(x)在区间
 上的最值.
上的最值.
【答案】分析:(1)先对函数 利用三角恒等变换公式进行化简,再利用周期公式求周期;
利用三角恒等变换公式进行化简,再利用周期公式求周期;
(2)根据化简后的三角函数解析式,令 ,k∈Z,从中解出x的取值范围,即可得到函数的单调递减区间;
,k∈Z,从中解出x的取值范围,即可得到函数的单调递减区间;
(3)由 得出
得出 的取值范围,然后再由正弦函数的性质求出
的取值范围,然后再由正弦函数的性质求出 的取值范围,即可得到函数f(x)在区间
的取值范围,即可得到函数f(x)在区间 上的最值.
上的最值.
解答:解: (4分)
(4分)
(1)最小正周期 ; (6分)
; (6分)
(2)当 ,即
,即 k∈Z时,
k∈Z时,
函数f(x)单调递减,
所以函数f(x)的单调递减区间为 . (10分)
. (10分)
(3)∵ ,∴
,∴ ,
,
∴
∴ . (14分)
. (14分)
点评:本题考查三角恒等变换的应用,解题的关键是熟练掌握三角恒等变换公式,利用公式对函数解析式进行化简,熟记三角函数周期的求法,单调区间的求法及最值的求法,本题是高考中对三角函数知识考查的常见题型,一般出现在高考试卷的第十七题的位置,属于中档题.
 利用三角恒等变换公式进行化简,再利用周期公式求周期;
利用三角恒等变换公式进行化简,再利用周期公式求周期;(2)根据化简后的三角函数解析式,令
 ,k∈Z,从中解出x的取值范围,即可得到函数的单调递减区间;
,k∈Z,从中解出x的取值范围,即可得到函数的单调递减区间;(3)由
 得出
得出 的取值范围,然后再由正弦函数的性质求出
的取值范围,然后再由正弦函数的性质求出 的取值范围,即可得到函数f(x)在区间
的取值范围,即可得到函数f(x)在区间 上的最值.
上的最值.解答:解:
 (4分)
(4分)(1)最小正周期
 ; (6分)
; (6分)(2)当
 ,即
,即 k∈Z时,
k∈Z时,函数f(x)单调递减,
所以函数f(x)的单调递减区间为
 . (10分)
. (10分)(3)∵
 ,∴
,∴ ,
,∴

∴
 . (14分)
. (14分)点评:本题考查三角恒等变换的应用,解题的关键是熟练掌握三角恒等变换公式,利用公式对函数解析式进行化简,熟记三角函数周期的求法,单调区间的求法及最值的求法,本题是高考中对三角函数知识考查的常见题型,一般出现在高考试卷的第十七题的位置,属于中档题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目